树

树的基本概念

树是n个节点的有限集合，是一种递归的数据结构

树的根节点没有前驱，此外，所有节点有且仅有一个前驱

基本术语

  • 祖先节点：除自身外，根节点到该节点路径上的节点均为自身的祖先节点
  • 节点的度：节点的孩子数
  • 树的度：树中节点度数最大值
  • 分支节点：节点度>0
  • 叶子节点：节点度=0
  • 节点的深度：根节点为1，依次往下
  • 节点的高度：和深度相反，从下往上数
  • 路径长度：两节点之间边的数量
  • 森林：m(m>0)棵互不相交树的集合。森林和树可以转换

区分 度为n的树 和 n叉树

两者都满足所有节点的度<=n

前者必须至少有一个节点度为n，后者可以不必有

前者不可以为空树，后者可以是空树

树的一些性质

  1. 树中的节点数 = 所有节点度数之和 + 1（根节点）
  2. 度数为m的树中，第i层上至多有 $m^{(i-1)}$ 个节点
  3. 高度h的m叉树最多有 $\frac{(m^h-1)}{(m-1)}$ 个节点
    1
    2
    3
    4
    5
    6
    7
    证明：

    让所有非叶子节点度都为m，可以得到节点数最多的情况。进行一个等比数列求和

    1+m+m^2+...+m^(h-1) = 1*(1-m^h)/(1-m)

    证毕
  4. 具有n个节点的m叉树最小高度为 $\lceil \log_m{n(m-1)+1)} \rceil$
    1
    2
    3
    4
    5
    6
    7
    8
    9
    证明：

    让所有非叶子节点的度都尽量为m，可以让树高度最小

    假设结果有h层，那么n>(h-1)层m叉树最大节点数，n<=h层m叉树最大节点数，即

    (m^(h-1)-1)/(m-1) < n < (m^h-1)/(m-1)

    同 *(m-1), 对m取log 即证得 h

例题

1
2
3
4
5
一棵度为4的树中，有20个节点度为4，10个度为3，1个度为2，10个度为1，问叶子节点个数

解答：利用性质1
n = n0+n1+n2+n3+n4 = 0*n0+1*n1+2*n2+3*n3+4*n4
解得 n0 = 82

二叉树

二叉树定义和主要特性

定义

二叉树是另一种树形结构，特点是每一个节点至多有两棵子树，即二叉树中不存在度大于2的节点，并且二叉树的子树有序

区别：度为2的有序树

特殊的二叉树

  • 满二叉树：高度为h，且节点数为 $2^h-1$ 的二叉树
  • 完全二叉树：懂得都懂｜堆结构就是完全二叉树
    • 最多只有一个度为1的节点（做题会用到
  • 二叉排序树（BST）：左子树的节点的关键字都小于根节点的关键字；右子树的节点的关键字都大于根节点的关键字；左右子树又各自是二叉排序树
  • 平衡二叉树：树上任意节点的左右子树的深度之差不超过1
    • 可以有更高的搜索效率

二叉树的性质

  • 非空二叉树的叶子节点数等于度为2的节点数加上1 即 $n_0=n_2+1$
    1
    2
    3
    4
    证明：
    n = n0 + n1 + n2
    n = n1 + 2*n2 +1
    两式相减即证
  • 非空二叉树第k层最多有 $2^{(k-1)}$ 个节点
  • 高度h的二叉树最多有 $2^h-1$ 个节点（等比数列求和得到
  • 具有n个节点的完全二叉树的高度h为 $\lceil log_2{(n+1)}\rceil$

常见考点：

  • 对于一个完全二叉树，可以由总节点数n推出n0、n1和n2
    • n1只能是0或1
    • n0 = n1+1 所以，n0+n2一定是奇数
    • 那么就可以推导出
      • 如果完全二叉树有2k个节点，那么 n1 = 1, n0 = k, n2 = k-1
      • 如果完全二叉树有2k-1个节点，那么 n1 = 0, n0 = k, n2 = k-1
  • 完全二叉树的节点i所在层次： $\lfloor log_2{i}\rfloor+1$

二叉树的存储结构

  • 顺序存储结构：利用数组，需要存储空节点（造成浪费

    可以利用下标信息得到孩子、父亲信息

    假设从下标1开始存储

    左孩子—2i 右孩子—2i+1 父亲— $\lfloor \frac{i}{2}\rfloor 2$

    实际上，只适用于存储完全二叉树

  • 链式存储结构：二叉链，设置data，lchild和rchild域

    1
    2
    3
    4
    struct BiTNode{
        ElemType data;
        BiTNode *lchild, *rchild;
    };

    n个节点的二叉链表共有n+1个空链域（可以构造线索二叉树

二叉树的遍历和线索二叉树

二叉树的遍历

根据根节点N，左子树L和右子树R的访问顺序，可以有三种遍历，均可递归或非递归实现

先序遍历 NLR

递归算法

1
2
3
4
5
6
7
void PreOrder(BiTree T){
    if(T){
        visit(T);
        PreOrder(T->lchild);
        PreOrder(T->rchild);
    }
}

非递归算法

用一个栈模拟函数调用栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void PreOrder2(const BiTree& T){
    std::stack<BiTree> stk;
    BiTree p = T;
    while(p || !stk.empty()){
        if(p){
            std::cout<<p->data<<' ';
            stk.push(p);
            p = p->lchild;
        }else{
            p = stk.top();
            stk.pop();
            p = p->rchild;
        }
    }
}

中序遍历 LNR

递归算法

1
2
3
4
5
6
7
void InOrder(BiTree T){
    if(T){
        InOrder(T->lchild);
        visit(T);
        InOrder(T->rchild);
    }
}

非递归算法

和前序遍历的区别只在于访问节点的时机

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void InOrder2(const BiTree& T){
    std::stack<BiTree> stk;
    auto p = T;
    while(p || !stk.empty()){
        if(p){
            stk.push(p);
            p = p->lchild;
        }else{
            p = stk.top();
            std::cout<<p->data<<' ';
            stk.pop();
            p = p->rchild;
        }
    }
}

后序遍历 LRN

递归算法

1
2
3
4
5
6
7
void PostOrder(BiTree T){
    if(T){
        PostOrder(T->lchild);
        PostOrder(T->right);
        visit(T);
    }
}

非递归算法

  • 用两个栈（左神的做法，有点投机取巧了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void PostOrder2(const BiTree& T){
    std::stack<BiTree> stk1, stk2;
    stk1.push(T);
    while(!stk1.empty()){
        auto top = stk1.top();
        stk1.pop();
        stk2.push(top);
        if(top->lchild) stk1.push(top->lchild);
        if(top->rchild) stk1.push(top->rchild);
    }
    while(!stk2.empty()){
        auto top = stk2.top();
        stk2.pop();
        std::cout<<top->data<<' ';
    }
}
  • 用一个栈（这种比较正统 要认真理解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void PostOrder(const BiTree& T){
    std::stack<BiTree> stk;
    BiTree pre = nullptr;   // 用来保存上次遍历的节点
    while(T || !stk.empty()){
        // 先向左走到底
        while(T){
            stk.push(T);
            T = T->lchild;
        }
        T = stk.top();  // 取出栈顶进行处理
        stk.pop();
        if(T->rchild == nullptr || T->rchild == pre){   // 右子树为空或者已经遍历完，就该遍历当前节点，也就是根节点
            std::cout<<T->data<<' ';
            pre = T;    // 记录上一个节点
            T = nullptr;    // 跳过左走的代码，往上边回溯
        }else{
            stk.push(T);    // 右子树还没处理，根节点入栈，遍历完右子树再进行处理
            T = T->rchild;  // 去遍历右子树
        }
    }
}

层序遍历

从上到下一层一层遍历，每层都是从左到右。需要借助队列实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void LevelOrder(BiTree T){
    InitQueue(Q);
    BiTree p;
    EnQueue(Q, T);
    while(!IsEmpty(Q)){
        DeQueue(Q, p);
        visit(p);
        if(p->lchild){
            EnQueue(Q, p->lchild);
        }
        if(p->rchild){
            EnQueue(Q, p->rchild);
        }
    }
}

由遍历序列构建二叉树

中序 + 先序 / 后序 可以唯一确定一棵二叉树

先序 + 后序 则不可以

  • 前序遍历中，第一个节点为根节点
  • 后序遍历中，最后一个节点为根节点
  • 找到根节点后，在中序遍历中可以划分出左右子树。不断划分就可以还原出二叉树

线索二叉树

线索二叉树的基本概念

一棵树遍历得到序列后，每个节点（除了首尾）在序列中都有一个前驱和后继。传统二叉链表只能体现父子关系，不能直接得到遍历后序列中的前驱和后继信息

为了加快查找前驱和后继的速度，考虑将二叉链表中n+1个空链域利用起来

规定：如果没有左孩子，则存储前驱节点；如果没有右孩子，则存储后继节点

因此需要两个标志域表明指向的是孩子还是前驱后继

1
2
3
4
5
6
7
lchild
ltag = 0 指向左孩子
ltag = 1 指向前驱

rchild
rtag = 0 指向右孩子
ratg = 1 指向后继
1
2
3
4
5
6
// 线索二叉树节点的结构
typedef struct ThreadTNode{
    ElemType data = 0;
    ThreadTNode *lchild = nullptr, *rchild = nullptr;
    int ltag = 0, rtag = 0;
}ThreadTNode, *ThreadTree;

指向前驱和后继的指针，称为线索

建立线索二叉树

线索的信息只能在遍历的过程中得到，所以建立线索二叉树其实就是一个遍历的过程

建立中序线索二叉树的实现如下：需要借助一个pre指针指向遍历的前一个节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 中序遍历过程
void InOrder(ThreadTree& T, ThreadTree& pre){
    if(T){
        InOrder(T->lchild, pre);
        // 前驱线索
        if(T->lchild == nullptr ){
            T->ltag = 1;
            T->lchild = pre;
        }
        // 后继线索
        if(pre != nullptr && pre->rchild == nullptr){
            pre->rtag = 1;
            pre->rchild = T;
        }
        pre = T;
        InOrder(T->rchild, pre);
    }
}
// 建立中序线索二叉树
void creatInOrderThreadTree(ThreadTree& T){
    ThreadTree pre = nullptr;   // 最左边节点没有左孩子
    if(T){
        InOrder(T, pre);
        // 处理遍历序列的最后一个节点
        pre->rchild = nullptr;
        pre->rtag = 1;
    }
}

前序线索二叉树 需要避免环路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void preOrder(ThreadTree root, ThreadTree pre){
    if(root){
        // 前驱线索
        if(root->lchild == nullptr){
            root->lchild = pre;
            root->ltag = 1;
        }
        // 后继线索
        if(pre && pre->rchild == nullptr){
            pre->rchild = root;
            pre->rtag = 1;
        }
        pre = root;
        if(root->ltag == 0) // 避免环路
            preOrder(root->lchild, pre);
        preOrder(root->rchild, pre);
    }
}

后序线索二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void postOrder(ThreadTree root, ThreadTree pre){
    if(root){
        postOrder(root->lchild, pre);
        postOrder(root->rchild, pre);
        // 前驱线索
        if(root->lchild == nullptr){
            root->lchild = pre;
            root->ltag = 1;
        }
        // 后继线索
        if(pre && pre->rchild == nullptr){
            pre->rchild = root;
            pre->rtag = 1;
        }
        pre = root;
    }
}

利用线索二叉树实现遍历

  • 中序遍历

关键在于找到中序遍历第一个节点，以及每个节点的中序遍历后继

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 找到中序遍历的第一个节点
// 子树最左边的节点就是第一个
ThreadTree firstNode(ThreadTree root){
    while(root->ltag == 0)  root = root->lchild;
    return root;
}
// 找到中序遍历的后继节点
ThreadTree nextNode(ThreadTree node){
    if(node->rtag == 1)   return node->rchild;  // 有后继线索 直接返回后继节点
    // 有右子树，那么右子树的最左边就是后继节点
    return firstNode(node->rchild);
}
// 中序遍历
void InOrder2(ThreadTree root){
    for(auto p=firstNode(root);p;p=nextNode(p)){
        std::cout<<p->data<<' ';
    }
}
  • 找到中序遍历的最后一个节点

子树最右边的节点就是

1
2
3
4
ThreadTree lastNode(ThreadTree node){
    while(node->rtag == 0)  node = node->rchild;
    return node;
}
  • 找到中序遍历的前驱

左子树中最右边的节点 就是中序遍历的前驱

1
2
3
4
ThreadTree preNode(ThreadTree root){
    if(root->lchild == 1)   return root->lchild;    // 有前驱线索，直接返回前驱
    return lastNode(root->lchild);
}

树的存储结构

双亲表示法

孩子表示法

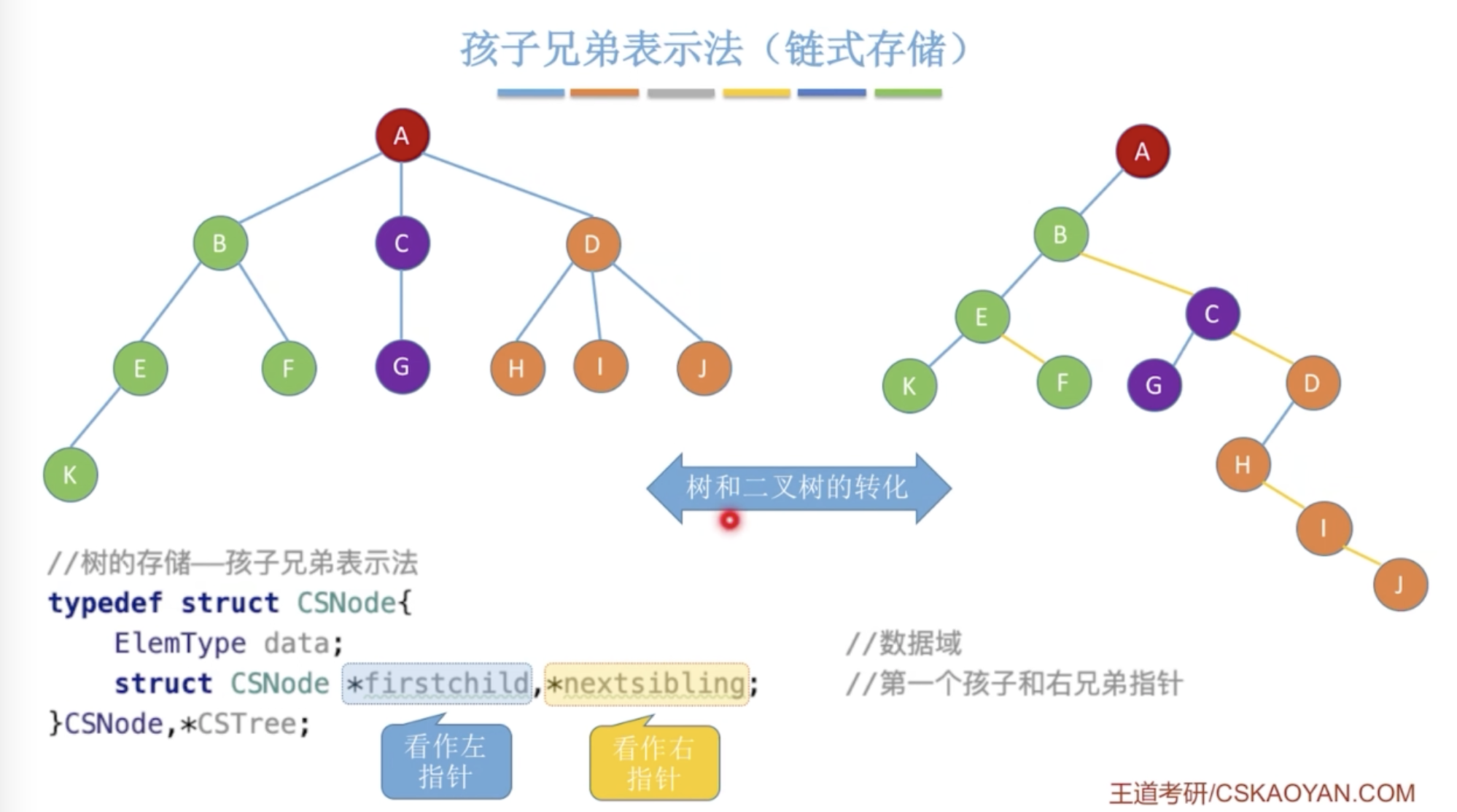
孩子兄弟表示法

涉及到树和二叉树的转换

森林和二叉树的转换也同理

孩子兄弟表示法 / 树转换为二叉树

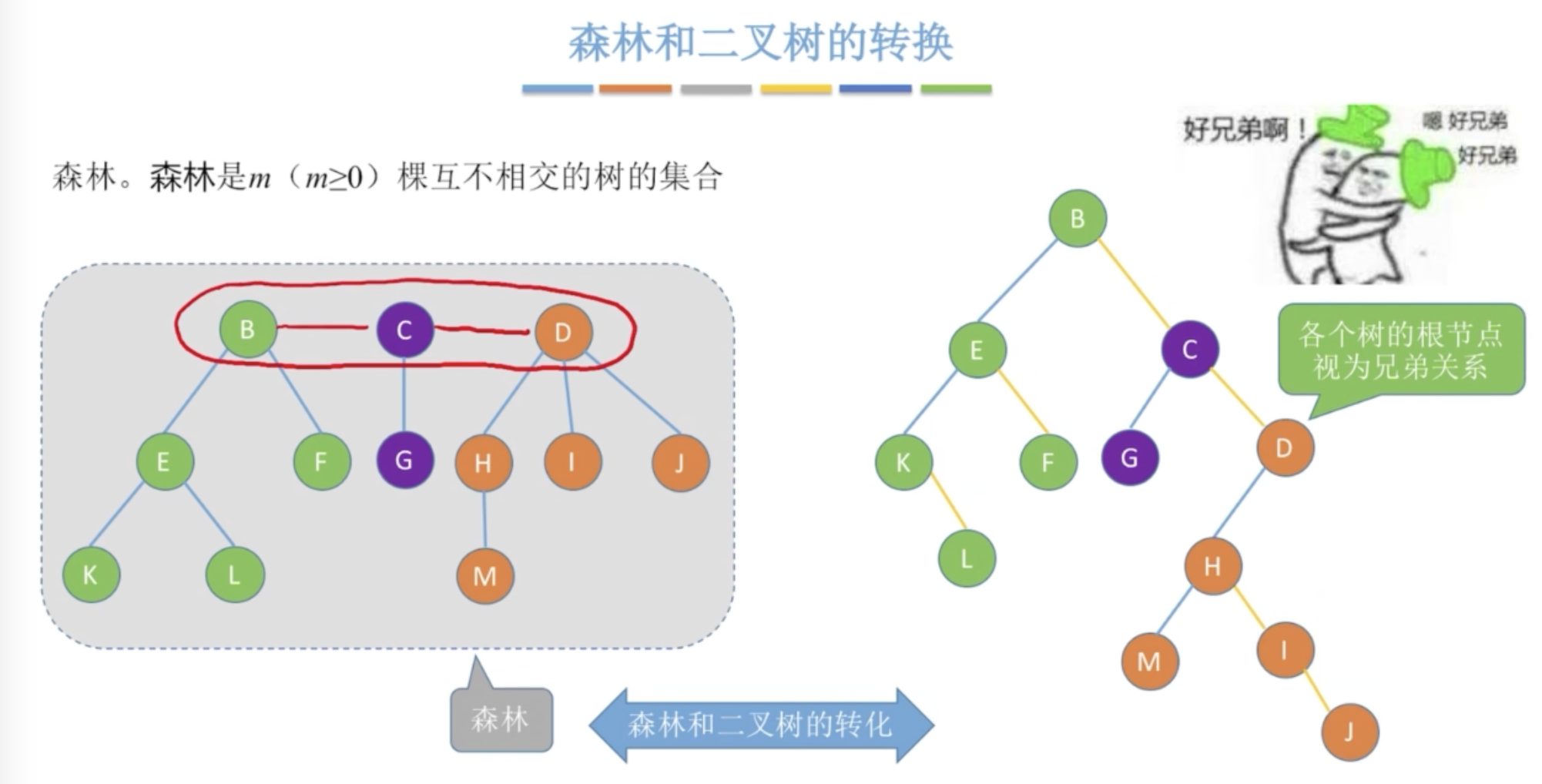
森林转换为二叉树

树的遍历

对树的遍历和对二叉树的遍历类似。分为先序遍历和后序遍历，均可以用递归实现

先序遍历

先访问根节点，再依次对每棵子树进行先序遍历

伪代码

1
2
3
4
5
6
7
8
void PreOrder(TreeNode* R){
    if(R){
        visit(R);
        while(R还有未访问子树T){
            PreOrder(T);
        }
    }
}

后序遍历

先对每棵子树进行后序遍历，再访问根节点

伪代码

1
2
3
4
5
6
7
8
void PostOrder(TreeNode* R){
    if(R){
        while(R还有未访问的子树T){
            PostOrder(T);
        }
        visit(R);
    }
}

层序遍历（广度优先遍历

借助一个队列

  1. 若树非空，将根节点入队
  2. while队列非空时，出队队头并访问，同时将其所有孩子入队
  3. 重复2直到队空

森林的遍历

这里只需要的到最后结果即可

  • 先序遍历：等于依次对所有树先序遍历的结果
  • 中序遍历：等于对所有树后序遍历的结果 / 对二叉树中序遍历的结果

二叉排序树 BST

定义：

  1. 左子树上所有节点的关键字都小于根节点的关键字
  2. 右子树上所有节点的关键字都大于根节点的关键字
  3. 左子树和右子树右各是一棵BST

特性：中序遍历可以得到递增的序列

二叉排序树的查找

从根节点出发，比较给定值和节点关键字，如果相等，则查找成功；如果给定值更小，则往左子树查找；否则往右子树查找

可以递归和非递归实现 空间复杂度上，非递归更优

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 非递归
BSTNode* BST_Search(BSTree T, int key){
    while(T && key != T->key){
        if(key < T->key){
            T = T->lchild;
        }else{
            T = T->rchild;
        }
    }
    return T;
}
// 递归
BSTNode* BST_Search(BSTree T, int key){
    if(!T)  return nullptr;
    if(key == T->key)   return T;
    else if(key < T->key)
        return BST_Search(T->lchild, key);
    else
        return BST_Search(T->rchild, key);
}

二叉排序树的插入

需要找到适合插入的位置。可以递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 递归
bool BST_Insert(BSTree& T, int k){
    if(!T){
        T = (BSTree) malloc(sizeof(BSTNode));
        T->key = k;
        T->lchild = T->rchild = nullptr;
        return true;
    }else if(k == T->key){
        return false;
    }else if(k > T->key){
        return BST_Insert(T->rchild, k);
    }else{
        return BST_Insert(T->lchild, k);
    }
}
// 非递归
bool BST_Insert2(BSTree T, int k){
    // 查找k
    // 找到k的话说明插入失败
    // 没找到k就构建一个k节点，链接一下即可
}

二叉排序树的构造

重要考点：给定一个序列，构造一棵二叉排序树

不同的序列得到的二叉排序树可能相等也可能不相等，查找的性能也有所差别。

平衡BST查找性能更好！

BST的删除

首先得找到节点Z

  • 如果Z是叶子节点 那么直接删除
  • 如果Z只有左子树或右子树，那么让孩子替代Z的位置就好
  • 如果Z有左右子树
    • 方案一：用Z的右子树中最小的节点Y替换Z的位置，再删除Y。因为Y位于右子树中最左，因此删除Y就是情况1或2
    • 方案二：用Z的左子树中最大的节点Y替换Z的位置，再删除Y。因为Y位于左子树中最右，因此删除Y就是情况1或2

BST查找效率

时间复杂度：O(log(2, h)) （对于AVL

所以h越小越好，即BST应该胖一点，那么就引出AVL（平衡二叉树）

平衡二叉树 AVL

定义

树上任意节点的左子树和右子树的高度之差不超过1

节点的平衡因子 = 左子树高 - 右子树高

对于AVL，所有节点的平衡因子只能取-1，0或1，绝对值都不会超过1

平衡二叉树的插入

一个重要的问题就是往平衡二叉树插入一个新节点后，如何保持平衡？

可以发现，插入一个新节点后，只需要向上找到第一个平衡因子不满足条件的节点，调整这棵子树就可以恢复平衡。这棵子树称为最小不平衡子树

分为四种情况

在A的左孩子的左子树插入新节点导致A不平衡

LL

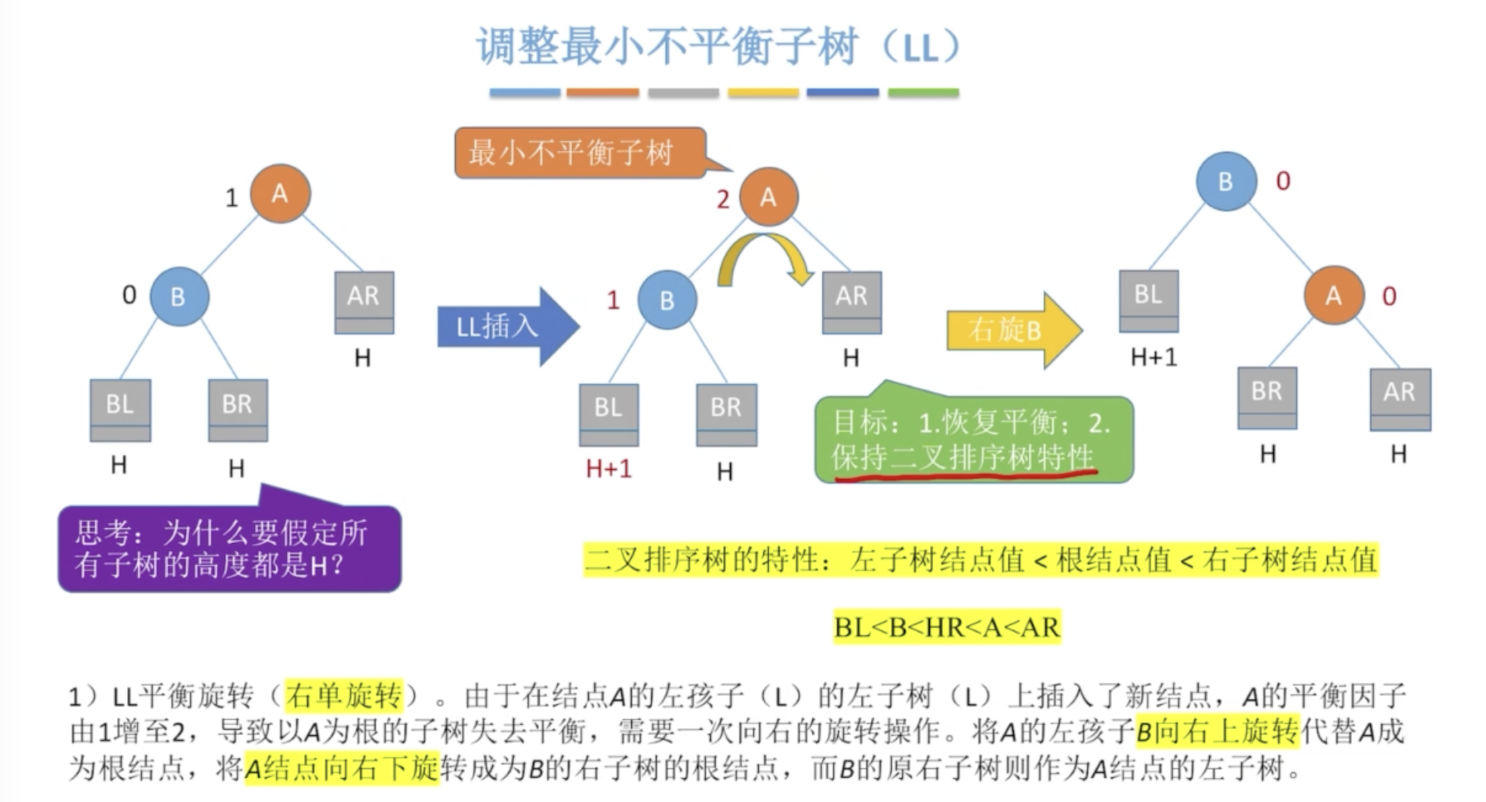
代码实现思路

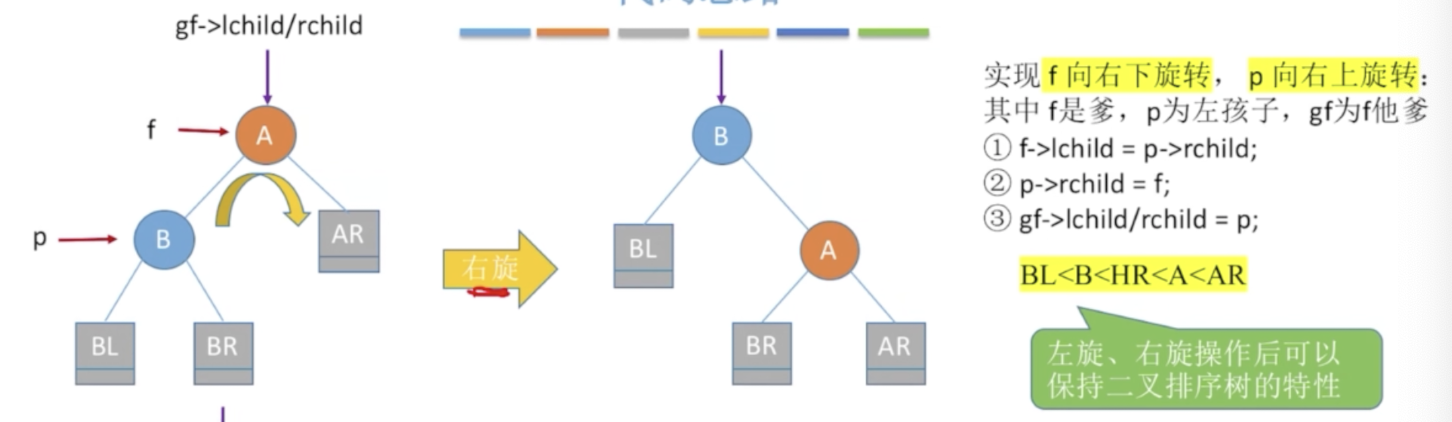
在A的右孩子的右子树插入新节点导致A不平衡

RR

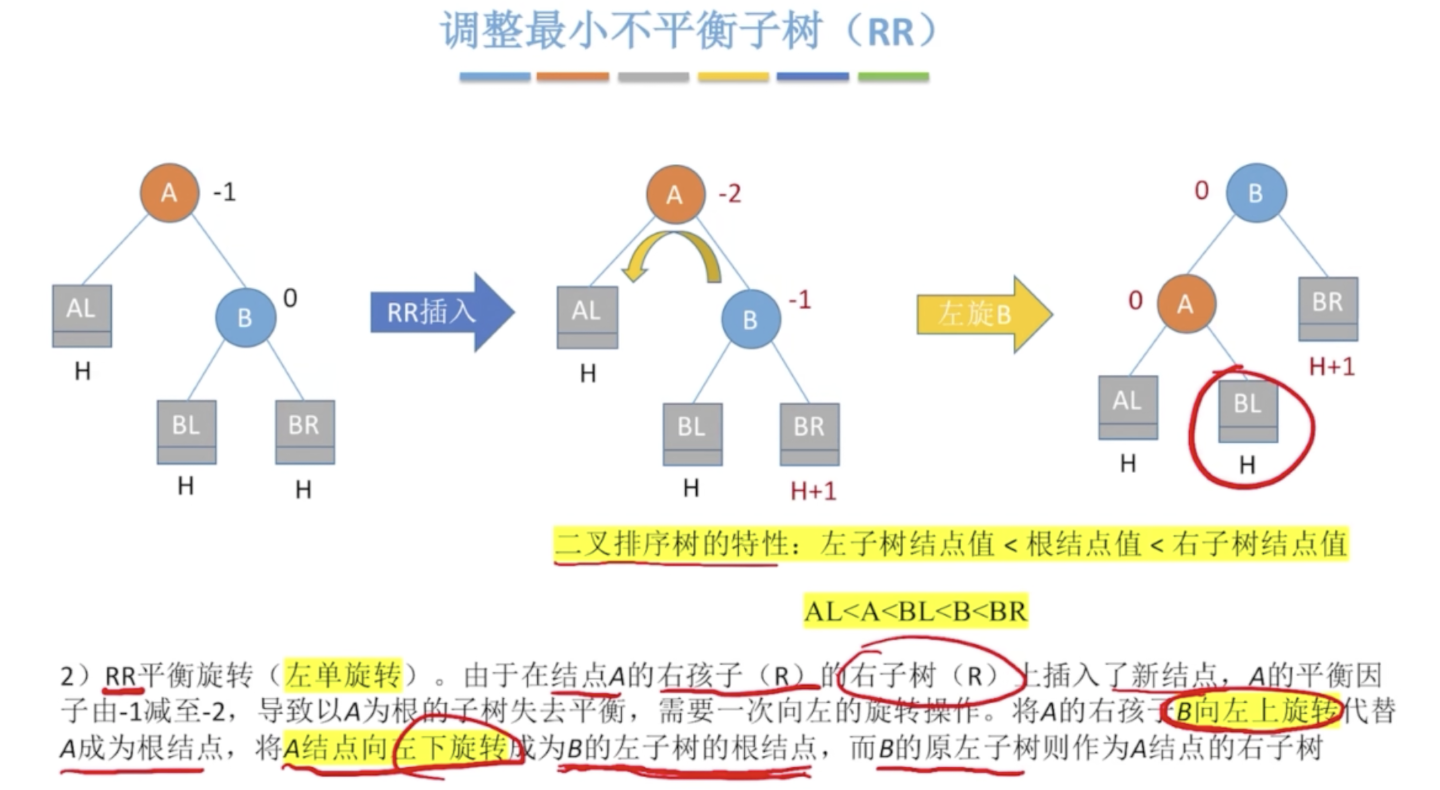
代码实现思路

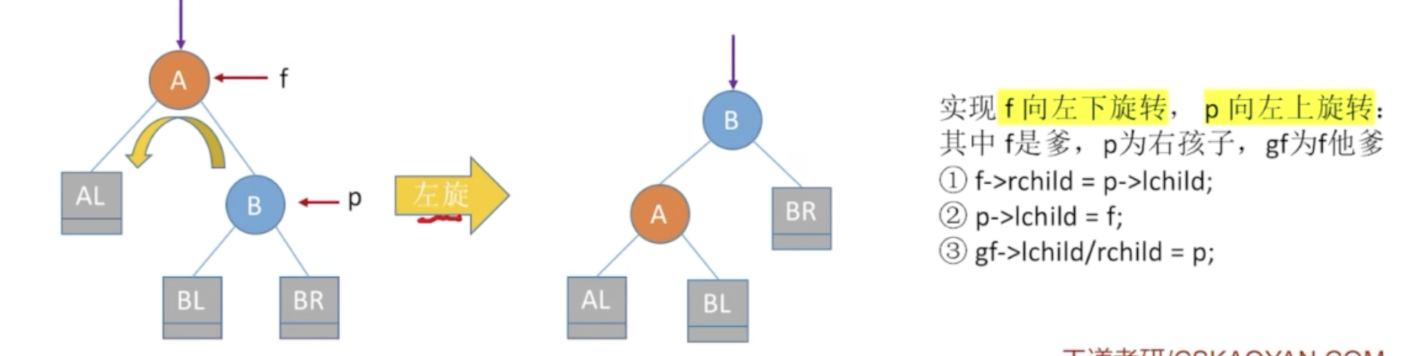
在A的左孩子的右子树插入新节点导致A不平衡

在A的右孩子的左子树插入新节点导致A不平衡

哈夫曼树

定义

  • 树的带权路径长度WPL：树中所有 叶子节点的权*根节点到叶子节点的路径长度 之和
  • 哈夫曼树：使WPL最小的二叉树。又称最优二叉树

哈夫曼树的特点：

  • 每个初始节点都成为叶子节点
  • 构造过程中生成了n-1个新节点，因此哈夫曼树的节点总数为2n-1
  • 哈夫曼树中不存在度为1的节点

构造哈夫曼树

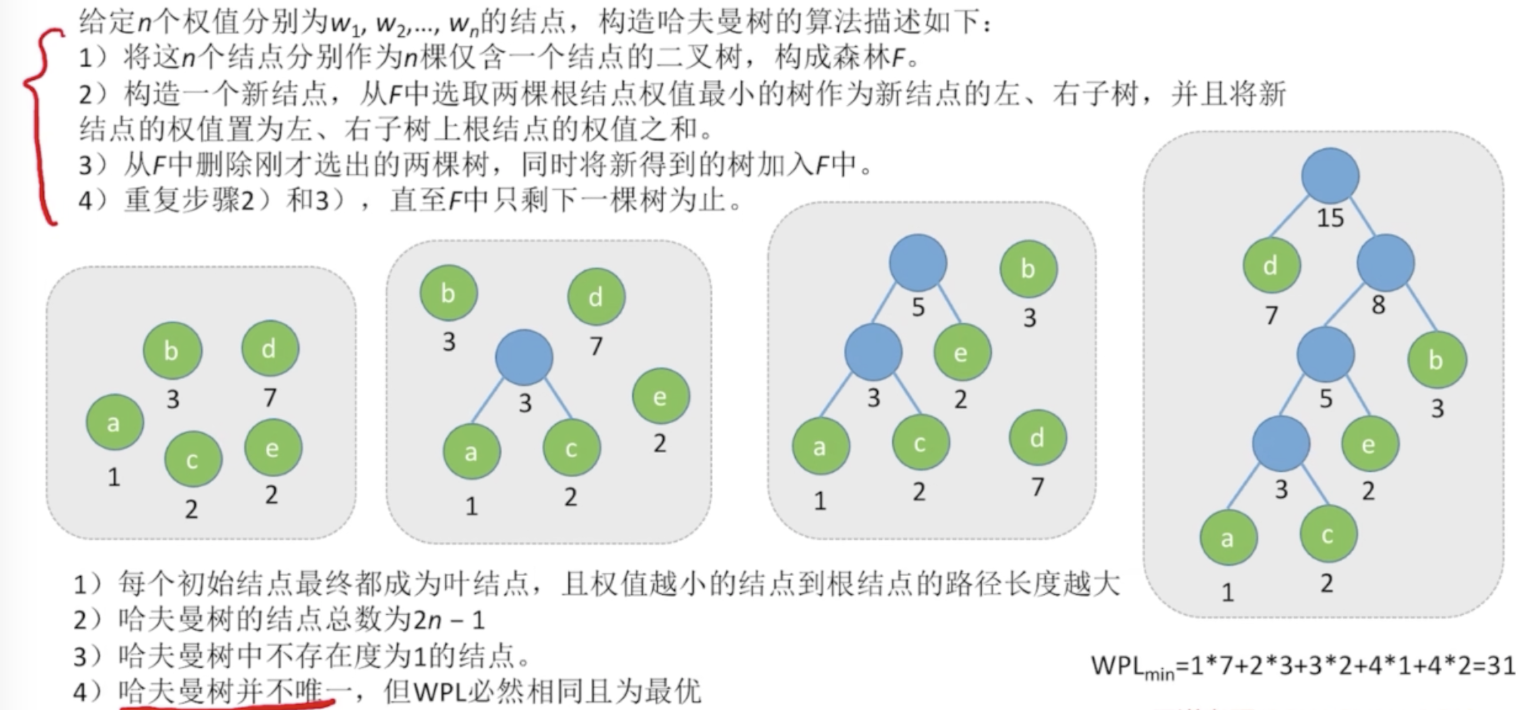
考点：哈夫曼编码 其实就是构造哈夫曼树，然后左0右1

用哈夫曼树可以设计出总长度最短的二进制前缀编码

赏

谢谢你请我吃糖果

支付宝
微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

一定要赢