leetcode 688. 骑士在棋盘上的概率

2022-02-17

题目

来做题

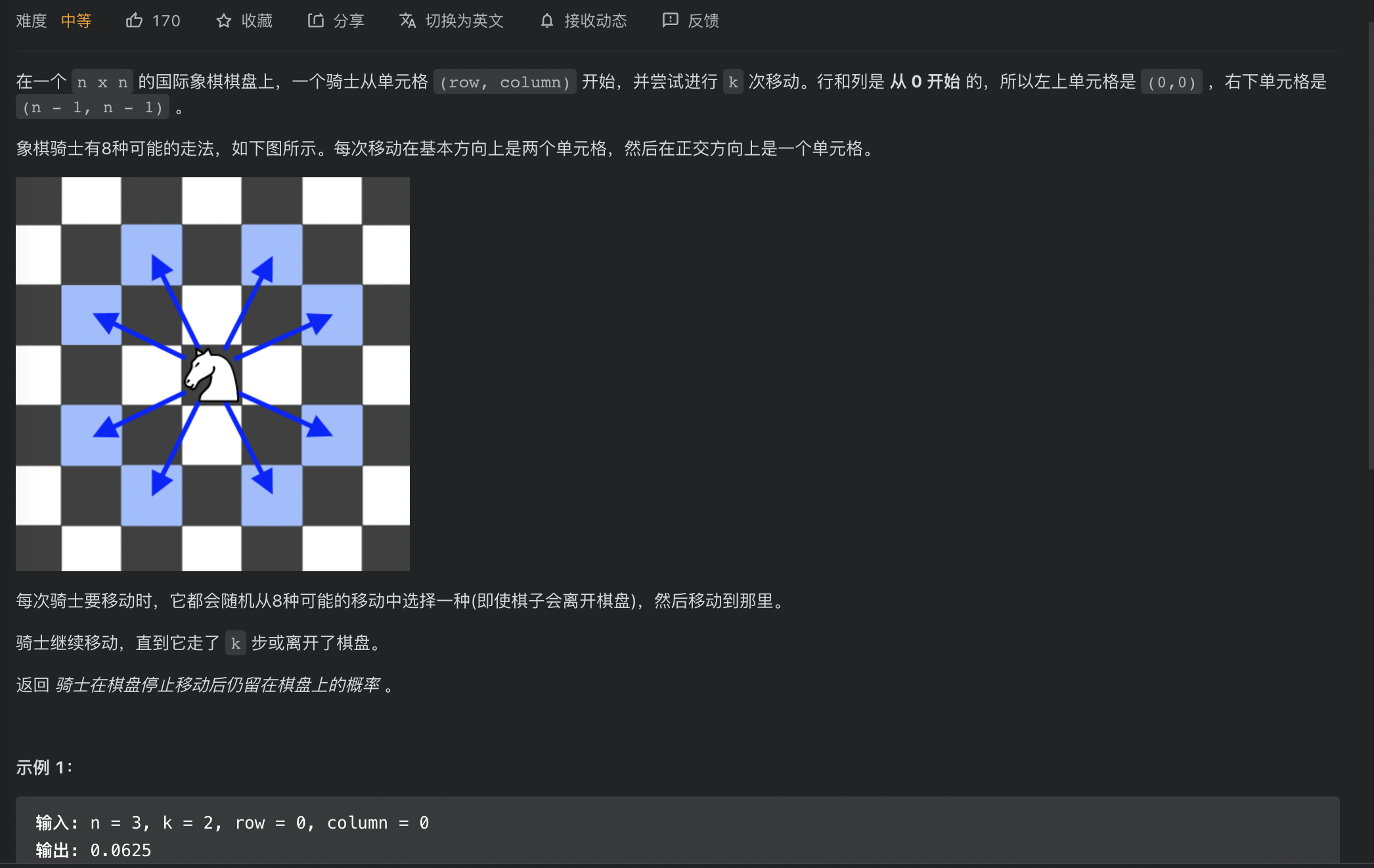
思路

动态规划：考虑到每走一步，结果与上一步的结果有关

定义dp[step][i][j] 表示骑士从i j出发，走了step步后还在棋盘上的概率

那么base case：dp[0][i][j] = 1。走了0步必定停留在棋盘上

状态转移方程呢？由于八个方向都相同概率会走，因此

dp[step][i][j] = 1/8 * SIGMA(dp[step-1][newi][newj])

SIGMA表示求和。转移方程指出：走step步后还在棋盘的概率等于走出一步后，在新位置走step-1步后仍在棋盘的概率

那么代码就简单明了了

技能点：动态规划

代码

class Solution {
    int dx[8] = {-2,-2,-1,1,2,2,1,-1};
    int dy[8] = {-1,1,2,2,1,-1,-2,-2};
public:
    double knightProbability(int n, int k, int row, int column) {
        // dp[step][i][j] 表示从ij出发，走了step步后仍在棋盘上的概率
        vector<vector<vector<double>>> dp(k+1, vector<vector<double>>(n, vector<double>(n)));
        // 规划！
        for(int step=0;step<=k;++step){
            for(int i=0;i<n;++i){
                for(int j=0;j<n;++j){
                    if(step == 0)   dp[step][i][j] = 1; // 走了0步，停留在棋盘上概率为1
                    else
                        for(int k=0;k<8;++k){           // 尝试八个方向
                            int nx = i+dx[k], ny = j+dy[k];
                            if(nx>=0 && nx<n && ny>=0 && ny<n){
                                dp[step][i][j] += dp[step-1][nx][ny]/8; // 状态转移
                            }
                        }
                }
            }
        }
        return dp[k][row][column];
    }
};