数制和计算

2.1.1 进位计数制

十进制计数法：

Kn,Kn-1,Kn-2,…,K0,K-1,K-2,…,K-m = SIGMA (i=-m ~ n) [Ki * 10^(i-1)]

二进制： 0 1

八进制： 0 1 2 3 4 5 6 7

十六进制 0 1 2 3 4 5 6 7 8 9 A B C D E F

真值 机器数

进制转换

• r进制转换为十进制：所有数值乘以各自位权之和

• 二进制转八进制：三位为一组

• 二进制转十六进制：四位为一组

• 十进制转r进制

  • 整数部分：除以r取余数，逆序
  • 小数部分：乘以r取整，正序 可能会有精度损失

2.1.2 BCD码

4个bit表示1个十进制字符

8421码

就是二进制 8421分别为位权。有6种冗余

985 = 1001,1000,0101

为了避免冗余状态的出现，进行加法可能需要+6进一位，进行减法可能需要-6

例如
  5  +   8   = 13
0101 + 1000  = 1101 + 0110 = 1 0011 

余3码

8421基础上+3

每一位数没有固定的权值，属于是无权码

2421码

权值分别是 2 4 2 1

为了不发生歧义，规定0-4的2421码第一位为0，5-9的第一位为1

字符和字符串

ASCII码

32～126 可印刷字符 其余为控制、通信字符

0~9 48（0011 0000）～ 57（0011 1001）：高4位相同，低四位为8421码

A~Z 65～90

a~z 97～122

汉字的表示和编码

GB 2312-80

包含区位码和位 数据传输可能出现问题（可能理解为ASCII的0-31

因此，区位码和位码都加上20H，得到国标码，可以避免和控制/通信字符冲突

汉字内码 = 国标码+80H

大小端

大端：多字节数据的高字节放在低地址

小端：多字节数据的低字节放在低地址

2.1.4 奇偶校验码

校验原理

• 码字：若干位代码组成的一个字称为码字
• 两个码字间的距离：两个码字逐位进行对比，不同的位的个数
• 一种编码方案可能有若干个合法码字，各合法码字之间的最小距离称为码距

例如编码：00 01 10 11 都是合法码字（码距为1），那么发生位错误时，就会被认为是另一个合法码字

如果增加一位校验位，编码：100 001 010 111，3bit映射到4个合法状态（码距位2），发生1bit错误时，就可以检验出来

奇偶校验码

奇校验码：整个校验码中，“1”的个数为奇数

偶校验码：整个校验码中，“1”的个数位偶数

假定最高位设置校验位

1001101 奇校验码：1,1001101 偶校验码：0,1001101
1010111 奇校验码：0,1010111 偶校验码：1,1010111

检错：用一种校验方案，发送方和接收方检验1的个数奇偶性

偶校验的硬件实现

各个信息位进行模2加运算，得到的结果就是偶校验位

模2加
0^0 = 0
1^1 = 0
1^0 = 1
0^1 = 1

偶数个1异或会变成0，若干个0异或还是0，而偶校验位也应该是0，

校验：所有位进行异或运算，结果为1说明出错

2.1.5 海明校验码

思想：多位校验位，可以携带对错信息，以及错误位置。实现检查、纠正错误

假设有n位信息位，k位校验位，k需要多少才行呢？
n+k位码，每一位都可能出错，k位可以携带2^k信息，所以
2^k >= n+k+1 才可以 1代表正确的

2^k >= n+k+1

校验位的分布：校验位Pi放在海明码中2^(i-1)的位置，下标从1开始

海明码求解步骤

海明码纠错

校验位和分组内的信息位进行异或

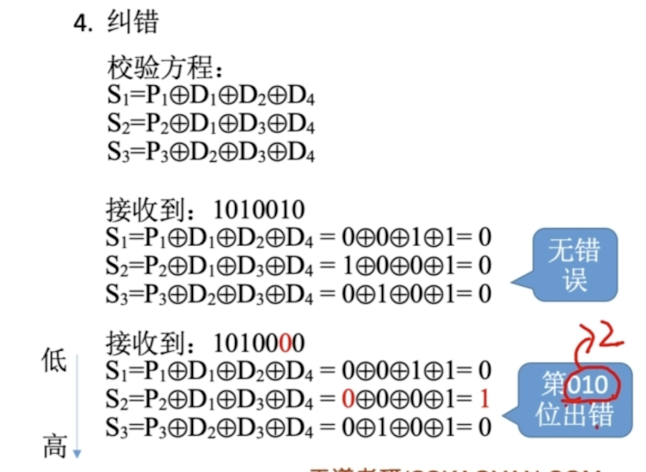
补充

海明码具有1位纠错能力，2位检错能力

2.1.6 循环冗余校验码 CRC

思想：数据的发送方和接受方约定一个“除数”

K个信息位+R个校验位作为“被除数”，添加校验位后需要保证除法的余数为0

2.2.1 定点数的表示

无符号数

通常只讨论无符号整数而不考虑无符号小数

整个机器字长的全部二进制位都是数值位，没有符号位，相当于绝对值

表示范围：0 ~ 2^n-1

有符号数的定点表示

定点整数：小数点位置隐含在最后，最高位为符号位

定点小数：小数点隐含在最高位后面，最高位为符号位

原码

尾数表示真值的绝对值，符号位 0/1 对应 正/负

机器字长n+1位的原码整数可以表示的范围是： -(2^n-1) ~ (2^n-1)

机器字长n+1位的原码小数可以表示的范围是： -(1-2^(-n)) ~ (1-2^(-n))

真值0有+0和-0两种形式

反码

正数的反码：和原码相同

负数的反码：符号位不变，数值位全部取反

由于和原码一一对应，所以他俩的表示范围也相同

补码

可以用加法替代减法，符号位参与运算，减少硬件开销

正数的补码：和原码相同

负数的补码：反码末位+1 考虑进位

注意：补码的真值0只有一种表示形式

[x]补 = 1,0000000 表示 x = -2^7

[x]补 = 1.0000000 表示 x = -1

小技巧：已知[x]补，求[-x]补：符号和数值位都取反，末位+1

移码

在补码的基础上将符号位取反

注意：移码只能用于表示整数

移码可以方便地比较大小

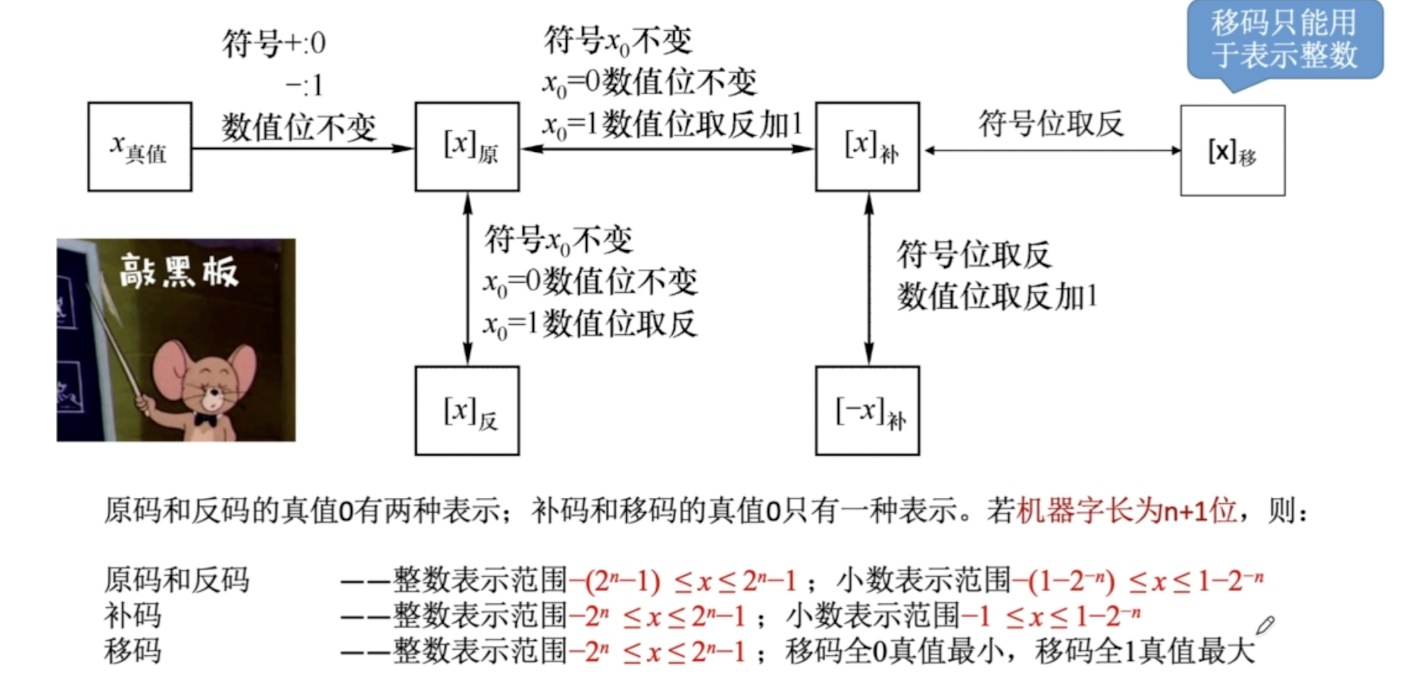
2.2.3 移位运算

算数移位

可以用于替代乘法和除法

原码的算数移位

符号位不变，仅对数值位进行移位

算数右移：高位补0，低位舍弃。如果舍弃位为0，则相当于除以2，否则会丢失精度

算数左移：低位补0，高位舍弃。舍弃0相当于乘以2，否则会丢失

反码的算数移位

正数的反码：右移补0，左移补0

负数的反码：右移补1，左移补1

补码的算数移位

正数的补码：右移补0，左移补0

负数的补码：右移，高位补1；左移低位补0、

逻辑移位

逻辑右移：高位补0，低位舍弃

逻辑左移：低位补0，高位舍弃

循环移位

循环左移：最高位移动到最低位

带进位位的循环左移：数值位最高位进入CF，CF进入最低位

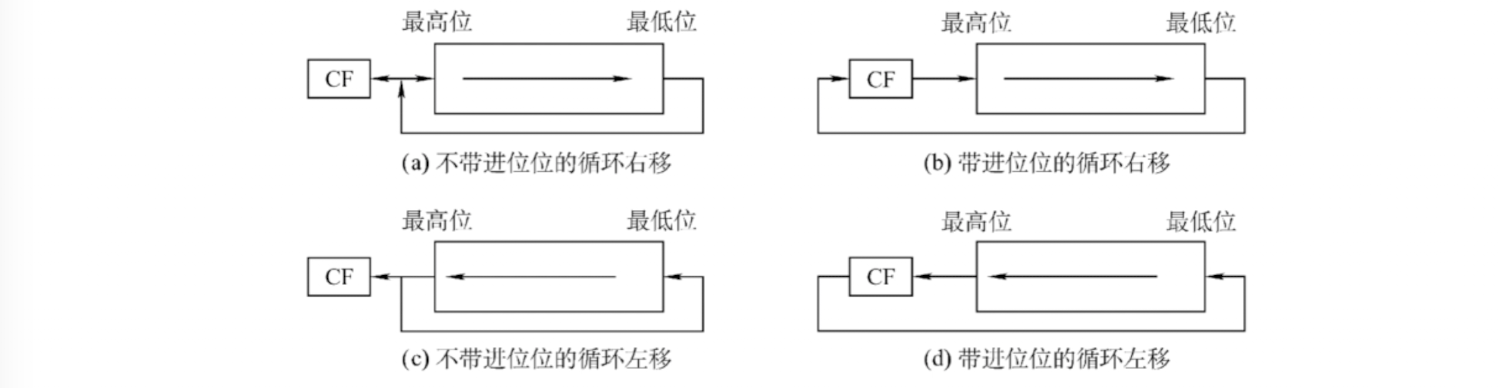
2.2.4 加减运算和溢出判断

补码加减运算

符号位参与运算

[A+B]补 = [A]补 + [B]补

[A-B]补 = [A]补 + [-B]补

小技巧：已知[x]补，求[-x]补：符号和数值位都取反，末位+1

当位数不够时，可能会发生溢出：上溢 / 下溢

溢出判断

只有 正数 + 正数 才可能上溢；负数 + 负数 才可能下溢

法一：采用一位符号位，通过符号位的情况

S = A + B，符号分别为 Sa, Sb, Ss

溢出的情况只有 (0, 0, 1) 和 (1, 1, 0)两种情况

真值表可以解出（数电知识）

V = SaSb(Ss)’ + (Sa)’(Sb)’Ss

V = 1 时溢出，V = 0 没有溢出

法二：采用一位符号位，通过进位情况判断

Cs表示符号位进位，C1表示最高数值位的进位

上溢：Cs = 0， C1 = 1

下溢：Cs = 1， C1 = 0

V = Cs ^ C1 （异或

V = 1 时溢出，V = 0 没有溢出

法三：双符号位

正数为00，负数为11

上溢：01

下溢：10

记 V = S1 ^ S2

V = 1 时溢出，V = 0 没有溢出

双符号位补码又称 模4补码；单符号位补码又称：模2补码

符号扩展

为了避免溢出，可以将短数据扩展为长数据

正整数：补0即可

负整数：原码补0，反码和补码补1

正小数：补0即可

负小数：原码和补码补0，反码补1

2.2.5 乘法运算

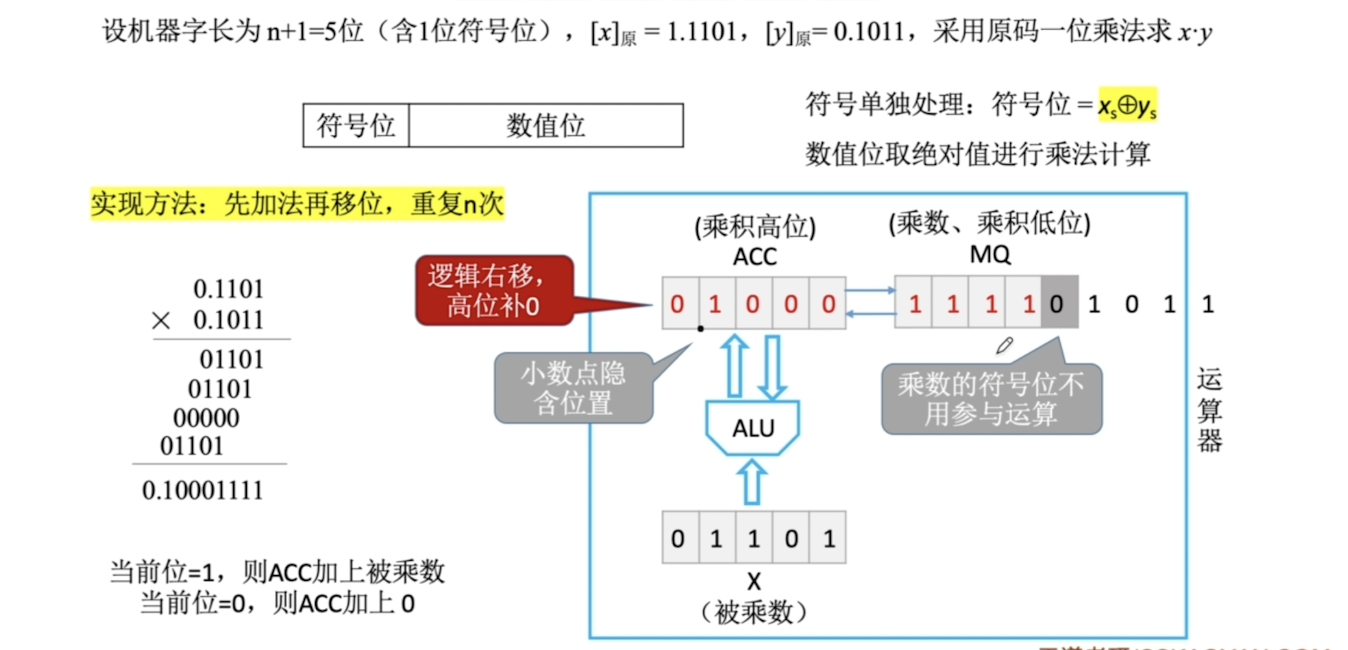
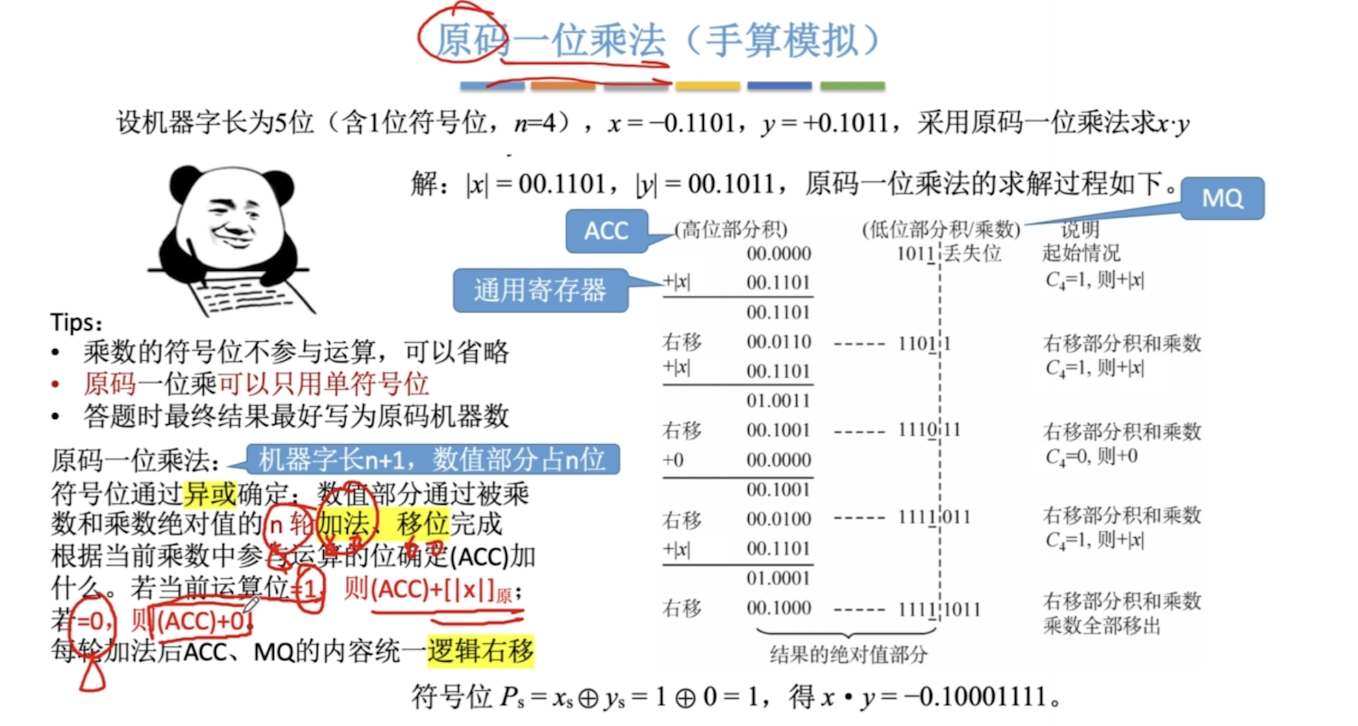
原码一位乘法

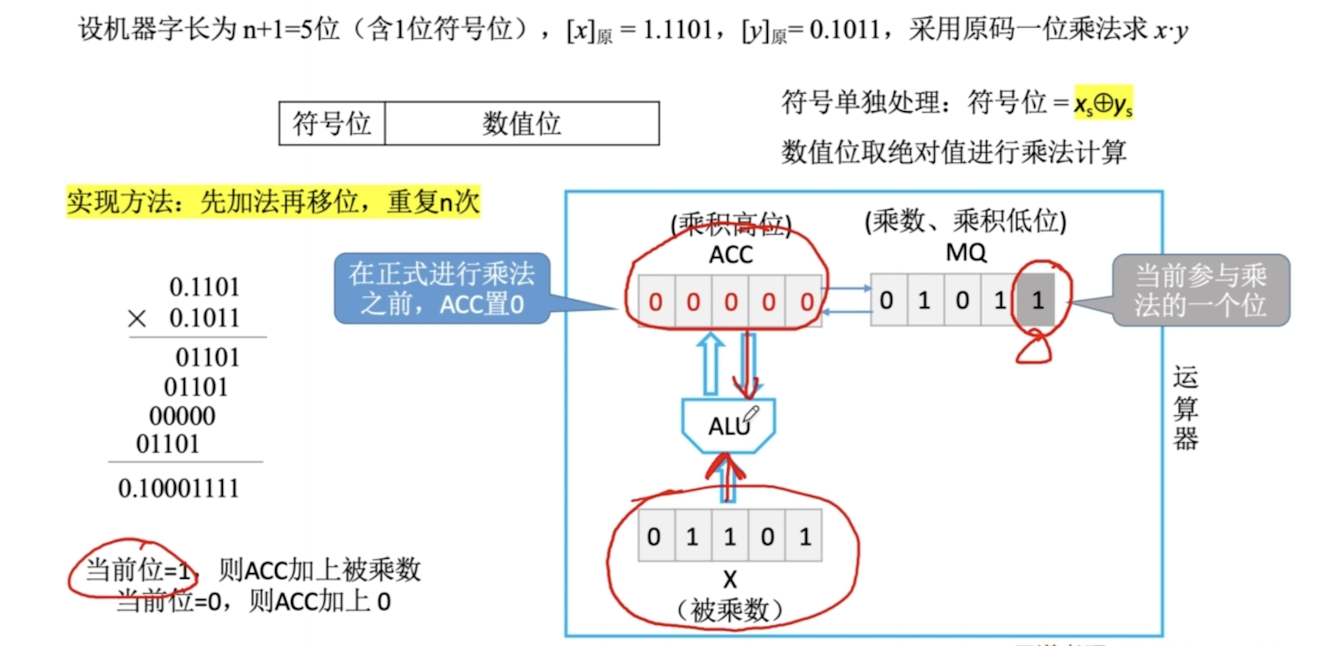
• ACC 结果的高位；MQ 被乘数，结果的低位；X乘数
• 符号位可以单独处理：S = Sx ^ Sy 数值位进行乘法
• MQ的最低位就是当前参与运算的位。1的话，ACC+X；0的话ACC+0
• 每次处理完一位，ACC和MQ整体逻辑右移（高位补0

补码一位乘法

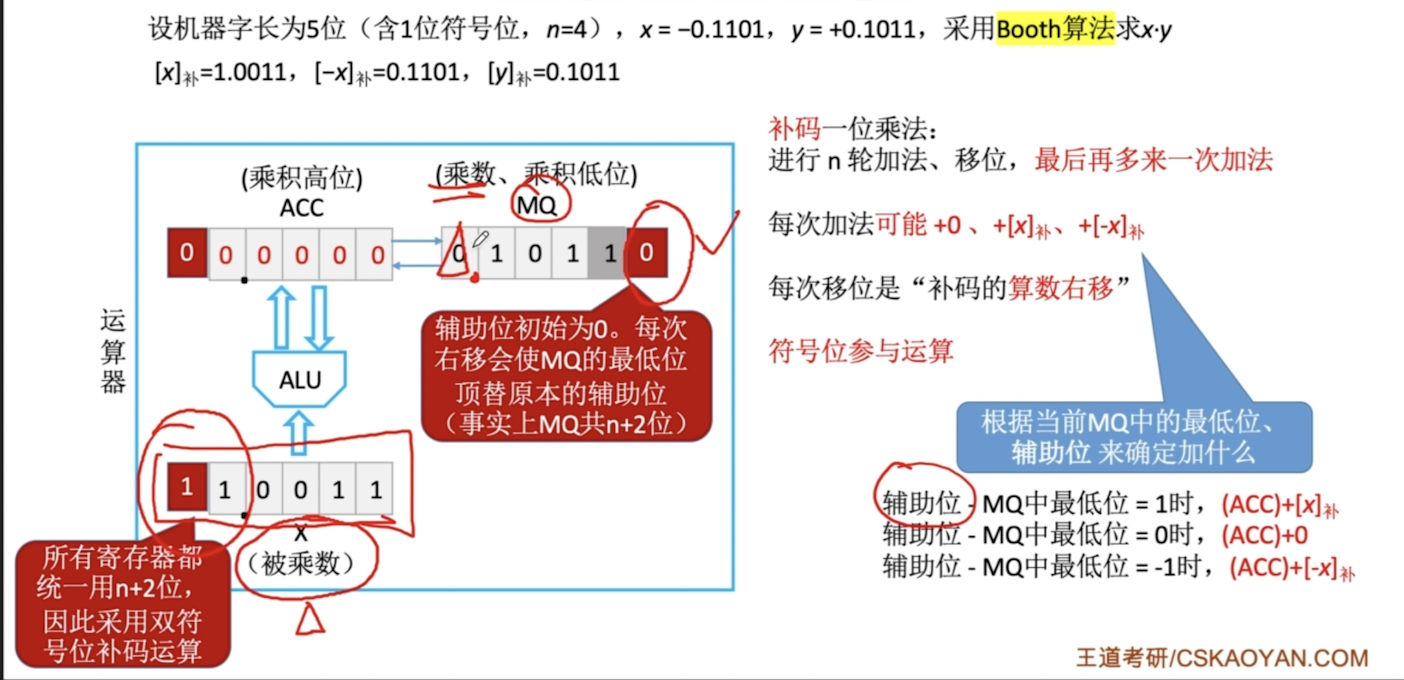
• 符号位参与运算
• 右移是算术右移
• 最后需要多一次加法
• 被乘数双符号位，乘数单符号位（+一位辅助），部分积双符号位

小技巧：已知[x]补，求[-x]补：符号和数值位都取反，末位+1

2.2.6 除法运算

原码除法

均为逻辑左移

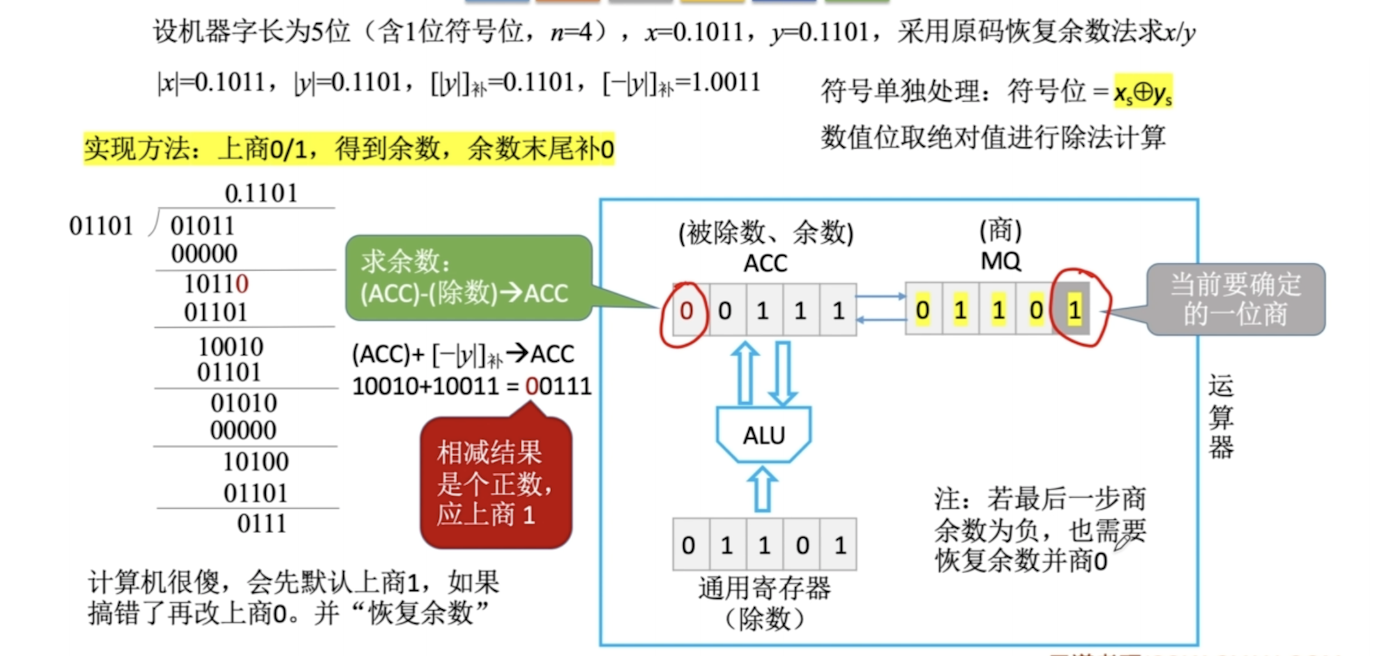
恢复余数法

• ACC 被除数、余数；MQ 商；X 除数
• 符号位单独处理 S = Sx ^ Sy
• 默认上商1，如果错了，再上商0，恢复余数
• 每次处理完一位，逻辑左移

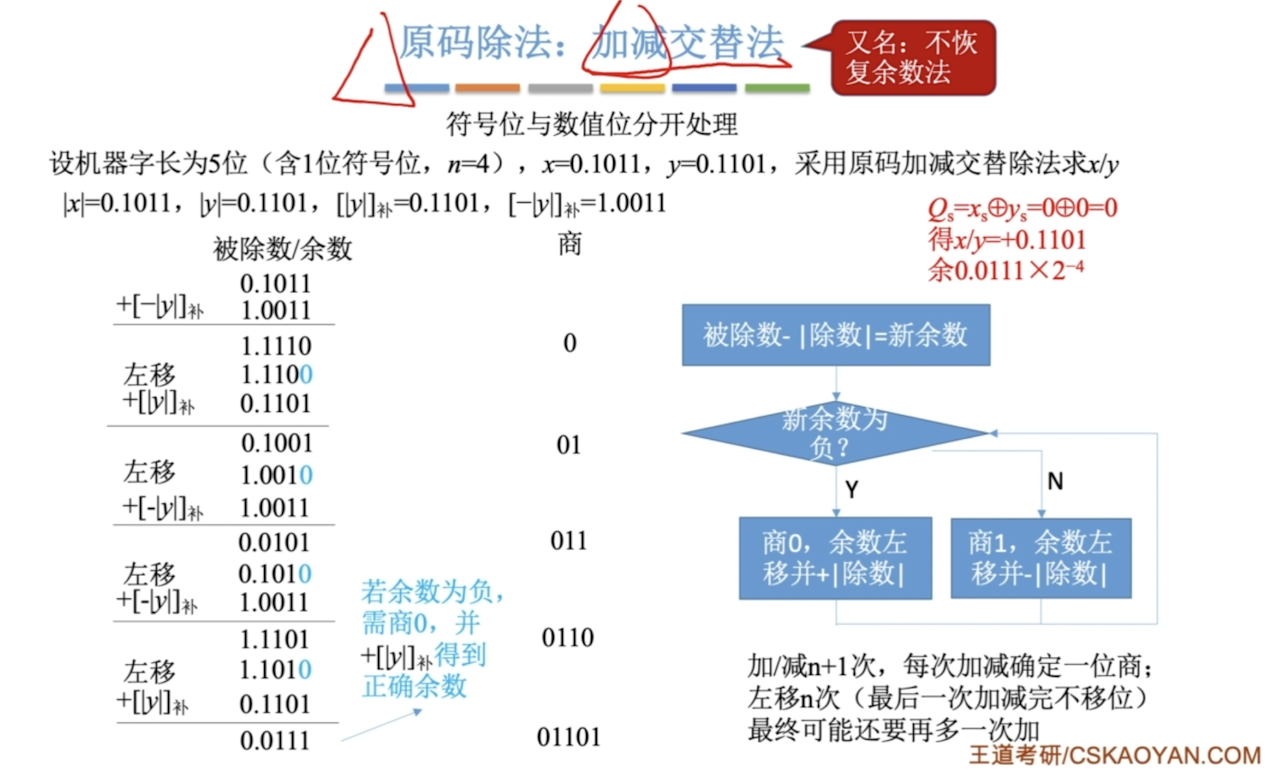
加减交替法

不恢复余数

第一个操作一定是减去除数的绝对值

• 余数为负，商0并左移，加上除数 得到新的余数
• 余数为正，商1并左移，减去除数 得到新的余数

补码除法

加减交替法

• 符号位参与运算
• 双符号位

1. 第一步：如果被除数和除数同号，则减掉除数；否则加上除数
2. 余数和除数同号，商1，余数左移一位减掉除数
3. 余数和除数异号，商0，余数左移一位加上除数
4. 重复n次
5. 末尾恒置为1

2.2.7 强制类型转换

C语言中定点整数用“补码”存储

1. 无符号和有符号整数转换，不改变数据内容，改变解释方式
2. 长整数转短整数，高位截断
3. 短整数变长整数：符号扩展

2.2.8 数据的存储和排列

大小端模式

多字节数据在内存中一定占据连续的几个字节

大端模式：高字节放在低地址

小端模式：低字节放在低地址

边界对齐

2.3.1 浮点数的表示

阶码E表示浮点数的表示范围以及小数点的实际位置

尾数M的数值部分位数反映浮点数的精度

浮点数尾数规格化

最终：让尾数的最高位是有效位

赏

谢谢你请我吃糖果

支付宝

微信