导数与微分

2022-02-24

2.1 导数的概念

引例应用题

$\frac{dA}{dB}$ A对B的瞬时变化率
切线斜率$f’(x_0)=k$ 法线斜率$-\frac{1}{f’(x_0)}$

定义

y=f(x) x∈D, x0∈D, x0+∆x∉D, ∆y=f(x0+∆x)-f(x0)
若 lim(∆x->0) ∆y/∆x 存在，称f(x)在x=x0可导，该极限称为f(x)在x=x0的导数，记作dy/dx|x=x0

导数的等价定义：$f’(x_0) = lim_{∆x\rightarrow{0}}\frac{f(x_0+∆x)-f(x_0)}{∆x} = lim_{x\rightarrow{x_0}}\frac{f(x)-f(x_0)}{x-x_0}$
1. 命题中$\Delta{x}$一般会被广义化
f(x)在某一点可导，则在该点出必定连续
导数存在的充要条件是左导数和右导数存在并相等
1. $f(x)=|x|$在$x=0$处导数不存在，切线不存在
2. 无穷导数视作导数不存在（光滑$\neq$可导
可导一定连续连续不一定可导
导数存在的等价说法
1. $y=f(x)$在$x_0$可导
2. $y=f(x)$在$x_0$导数存在
3. $f’(x_0)=A$，A为有限数

考点：函数在某一点的可导性

先看在该点是否连续，不连续一定不可导
求左右导数，看是否存在且相等

常用导数

求导的主要对象：初等函数

f(x)	f’(x)
C（常数）	0
x^n	n*x^(n-1)
a^x（a>0 && a!=1）	a^x * ln(a)
log(a, x)（a>0 && a!=1）	1/(x*ln(a))
sin x	cos x
cos x	-sin x

2.2 求导法则

四则运算法则

设u(x) v(x)可导
(u(x)+v(x))’ = u’(x)+v’(x)
(u(x)-v(x))’ = u’(x)-v’(x)
(u(x)v(x))’ = u’(x)v(x)+u(x)v’(x)
v(x)!=0时，(u(x)/v(x))’ = ((u’(x)v(x)-u(x)v’(x))/(v(x)^2))
推广：
(ku)’ = ku’ k为常数
(uvw)’ = u’vw + uv’w + uvw’

f(x)	f’(x)
tan x	sec^2(x)
cot x	-csc^2(x)
sec x	sec x * tan x
csc x	-csc x * cot x

反函数求导法则

前提：$y=f(x)$ 严格单调，才能有反函数

设$y=f(x)$可导并且$f’(x)\neq 0$（可知$f’(x)$必定恒为正或负），则其反函数$y=\phi(x)$可导
且 $\phi ‘(y) = \frac{1}{f’(x)}$

$f(x)$	$f’(x)$
$\arcsin x$	$\frac{1}{\sqrt{1-x^2}}$
$\arccos x$	$-\frac{1}{\sqrt{1-x^2}}$
$\arctan x$	$\frac{1}{1+x^2}$
$\arcctg x$	$-\frac{1}{1+x^2}$

二阶导数

$y_{xx}^{‘’}=-\frac{x_{yy}^{‘’}}{(x_{y}^{‘})^3}$

复合函数求导法则——链式法则

若y=f(u)可导，u=𝜙(x)可导且𝜙’(x)!=0，则y=f[𝜙(x)]可导，且dy/dx = f’[𝜙(x)]*𝜙’(x)

2.3 高阶导数

$f^{(n)}(x_0)=\lim_{\Delta{x}\rightarrow{0}}\frac{f^{(n-1)}(x_0+\Delta{x})-f^{(n-1)}(x_0)}{\Delta{x}}$

二阶及以上的导数称为高阶导数

方法一：归纳法

逐次求导，通过前几项，找出规律

y = sin x
可以归纳出 sin(x)^(n) = sin(x+(n𝛱)/2)

同理 cos(x)^(n) = cos(x+(n𝛱)/2)

$f(x)$	$f^{(n)}(x)$
$\sin{kx}$	$k^n\sin{[x+\frac{(n\pi)}{2}}]$
$\cos{kx}$	$k^n\cos{[x+\frac{(n\pi)}{2}]}$
$\frac{1}{ax+b}$	$(-1)^n n! a^n /(ax+b)^{n+1}$
$\frac{1}{x}$	$(-1)^nn!x^{-(n+1)}$
$\ln{x}$	$(-1)^{n-1}(n-1)!x^{-n}$
$\ln{(1+x)}$	$(-1)^{n-1}\frac{(n-1)!}{(1+x)^n}$
$(a^x)$	$a^x(\ln{a})^n$
$e^x$	$e^x$

方法二：公式法

莱布尼茨公式：

$(uv)^{(n)}=C^0_n u^{(n)}v+C^1_n u^{(n-1)}v^{(1)}+C^2_n u^{(n-2)}v^{(2)}+……+C^n_n uv^{(n)}$

其中

$C^m_n=\frac{n!}{m!\cdot(n-m)!}$

方法三：泰勒展开法

2.4 隐函数和参数方程确定的函数求导

隐函数

显函数：$y=f(x)$
隐函数：$F(x,y)=0$ 理论上可以求出 $y=f(x)$，但不一定解得出来。这个求解的过程叫做隐函数的显式化

隐函数求 $\frac{dy}{dx}$ 方法：$y$看成$y(x)$，两边同时对$x$求导

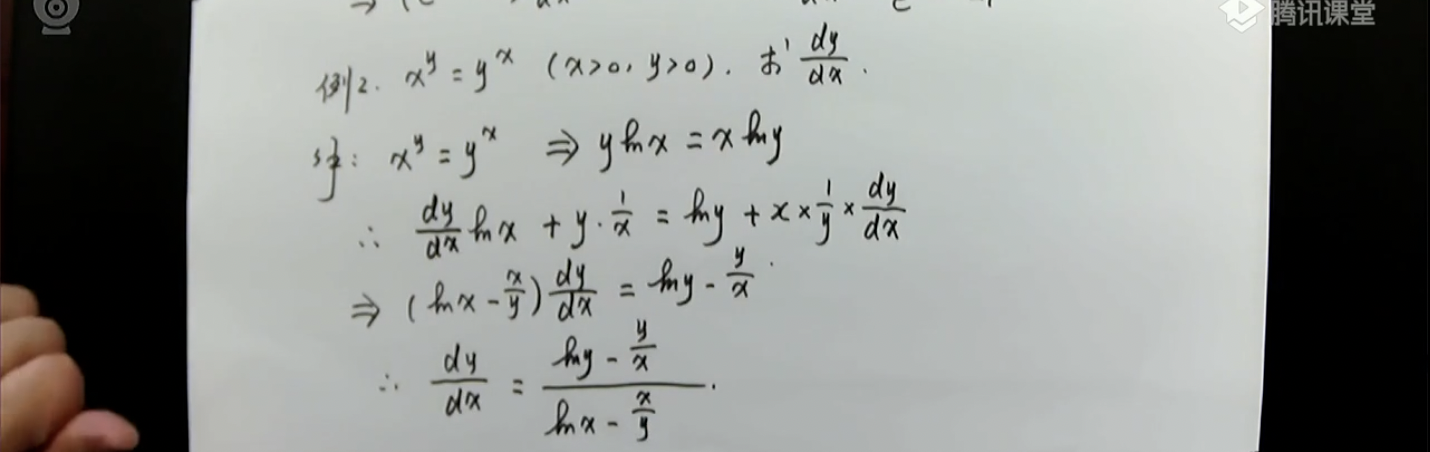
参数方程确定的函数求导

参数方程形如：

$f(x)=\left\{ \begin{aligned} x=\phi{(t)}\\ y=\psi{(t)}\\ \end{aligned} \right.$

确定了 $y=y(x)$。若$\phi{(t)}$ 和 $\psi{(t)}$ 可导，且$\phi{(t)\neq0}$

则$\frac{dy}{dx}=\frac{\psi^{‘}{(t)}}{\phi^{‘}{(t)}}$

$\frac{d^2y}{dx^2}=\frac{d(\frac{dy}{dx})}{dx}$ 同乘以$dt$ 可以推出 $\frac{d^2y}{dx^2}=\frac{d\frac{\frac{dy}{dx}}{dt}}{\phi’(t)}$

对数求导法

对于多项相乘、相除、开方、乘方的式子，一般先取对数再求导，可以简化计算

$\ln{y}=\ln{f(x)}$
$\frac{y’}{y}=\frac{f’(x)}{f(x)}$，则$y’=\frac{yf’(x)}{f(x)}$

幂指函数求导法

对于幂指函数$u(x)^{v(x)}, u(x)\neq{0}$，除了对数求导法，还可以转化为指数函数再求导

$[u(x)^{v(x)}]’=[e^{v(x)\ln{u(x)}}]’=e^{v(x)\ln{u(x)}}[v’(x)\ln{u(x)}+v(x)\frac{u’(x)}{u(x)}]$

2.5 微分

定义

$y=f(x),x\in{D},x_0+\Delta{x}\in{D},\Delta{y}=f(x_0+\Delta{x})-f(x_0)$，如果$\Delta{y} = A\Delta{x}+o(\Delta{x})$，则称$y=f(x)$在$x=x_0$可微，将$A\Delta{x}$称为在该点的微分
记作$dy|_{x=x_0}=A\Delta{x}=Adx$
由于$\Delta{x}=1·\Delta{x}+o(\Delta{x})$，根据定义，$\Delta{x}=dx$

可微的判别：

写增量：$\Delta{y}=f(x_0+\Delta{x})-f(x_0)$
写线性增量：$A\Delta{x}=f’(x_0)\Delta{x}$
做极限：$\lim_{\Delta{x}\rightarrow{0}}\frac{\Delta{y}-A\Delta{x}}{\Delta{x}}$，如果该极限为0，说明可微
1. $\Delta{y}=dy+o(\Delta{x})$
2. $dy|_{x=x_0}=A\Delta{x}=f’(x_0)\Delta{x}$

注解：

可导和可微等价
$A=f’(x_0)$
若 $y=f(x)$可导，则 $dy=df(x)=f’(x)dx$

一些数学意义

若一点可微，则该点附近可以用切线段近似代替曲线段

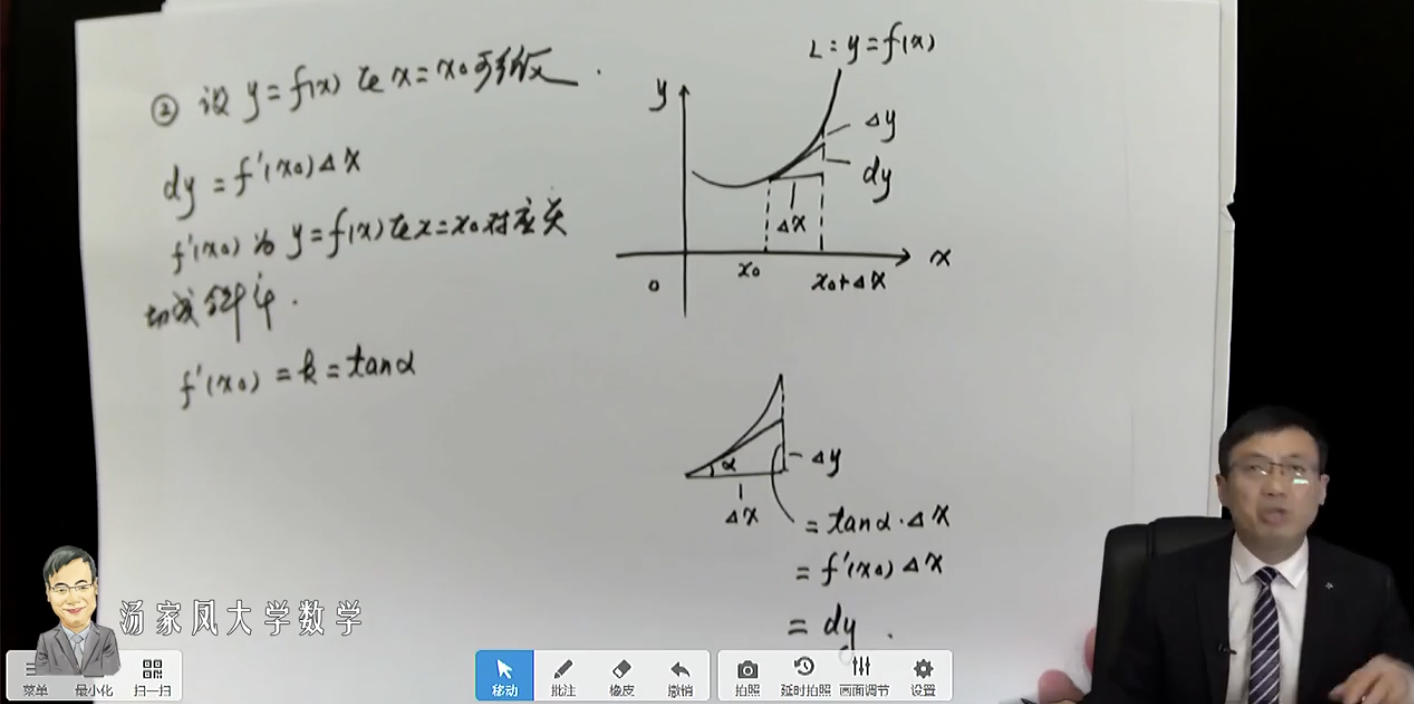
若 $y=f(x)$ 在 $x=x_0$ 可微，则 $\Delta{y}-dy=o(\Delta{x})$

一阶微分形式不变性

$df[\Delta]=f’(\Delta)d\Delta$

工具

公式

$f(x)$	$d(f(x))$
$C$	0
$x^a$	$ax^{a-1}dx$
$a^x$	$a^x\ln{a}dx$
$e^x$	$e^x$
$\log_a{x}$	$\frac{1}{x\ln{a}}dx$
$\ln{\x}$	$\frac{1}{x}$
$\sin{x}$	$\cos{x}dx$
$\cos{x}$	$-\sin{x}dx$
$\tan{x}$	$\sec^2{x}dx$
$\cot{x}$	$-\csc^2{x}dx$
$\sec{x}$	$\sec{x}\tan{x}dx$
$\csc{x}$	$-\csc{x}\cot{x}dx$
$\arcsin{x}$	$\frac{1}{\sqrt{1-x^2}}dx$
$\arccos{x}$	$-\frac{1}{\sqrt{1-x^2}}dx$
$\arctan{x}$	$\frac{1}{1+x^2}dx$
$arccot {x}$	$-\frac{1}{1+x^2}dx$

四则法则

$d(u \pm v)=du \pm dv$
$d(uv) = udv + vdu$
1. 注意逆用
3. 超过三个相乘的，一般谋求他法
$d(\frac{u}{v}) = \frac{vdu - udv}{v^2}$
1. 分母恒为非负数，考题可以只给分子形式

复合

一阶微分形式不变性：$y=f(u)$, $u=g(x)$,则 $dy=f’(u)du$

分段函数的导数

在分段点用导数定义求导，得到两个单侧导数，根据其关系判断是否存在
在非分段点用导数公式求导

$(\ln{|x|})’=\frac{1}{x}$，可以忽略绝对值

推广：$(\ln{u(x)})’=\frac{u’(x)}{u(x)}$

近似计算

$f(x_0+\Delta{x})\approx f(x_0)+f’(x_0)(x-\Delta{x})$

$f(x)\approx f(x_0)+f’(x_0)(x-x_0)$

例题：求 sin30.5 $\sqrt{1.04}=?$

考点

假设$f(x)$在$x=x_0$连续，且满足$\lim_{x\rightarrow{x_0}}\frac{f(x)}{x-x_0}=A$，则
- $f(x_0)=0$
- $f’(x_0)=A$
原函数若有奇偶性，则求一次导，奇偶性互换
- 求导偶数次，奇偶性不变
- 求导奇数次，寄偶性变
可导周期$T$函数的导函数也以$T$为周期

例题

$f(x)=\prod_{i=1}^{100}(\tan{\frac{\pi x^n}{4}-n})$，求$f’(1)$

后续内容结合

变限积分求导公式

设$F(x)=\int_{\phi_1{(x)}}^{\phi_2{(x)}}f(t)dt$，其中$f(x)$在$[a,b]$上连续，可导函数$\phi_1{(x)}$和$\phi_2{(x)}$值域在$[a,b]$上，则：

$F’(x)=\frac{d}{dx}[\int_{\phi_1{(x)}}^{\phi_2{(x)}}f(t)dt]=f[\phi_2{(x)}]\phi_2’(x)-f[\phi_1{(x)}]\phi_1’(x)$

具体地

$F’(x)=\frac{d}{dx}[\int_{a}^{x}f(t)dt]=f(x)$

$F’(x)=\frac{d}{dx}[\int_{a}^{\phi{(x)}}f(t)dt]=f[\phi{(x)}]\phi ‘{(x)}$