函数图像

直角坐标系下的图

常见图像

基本初等函数和初等函数

常数函数

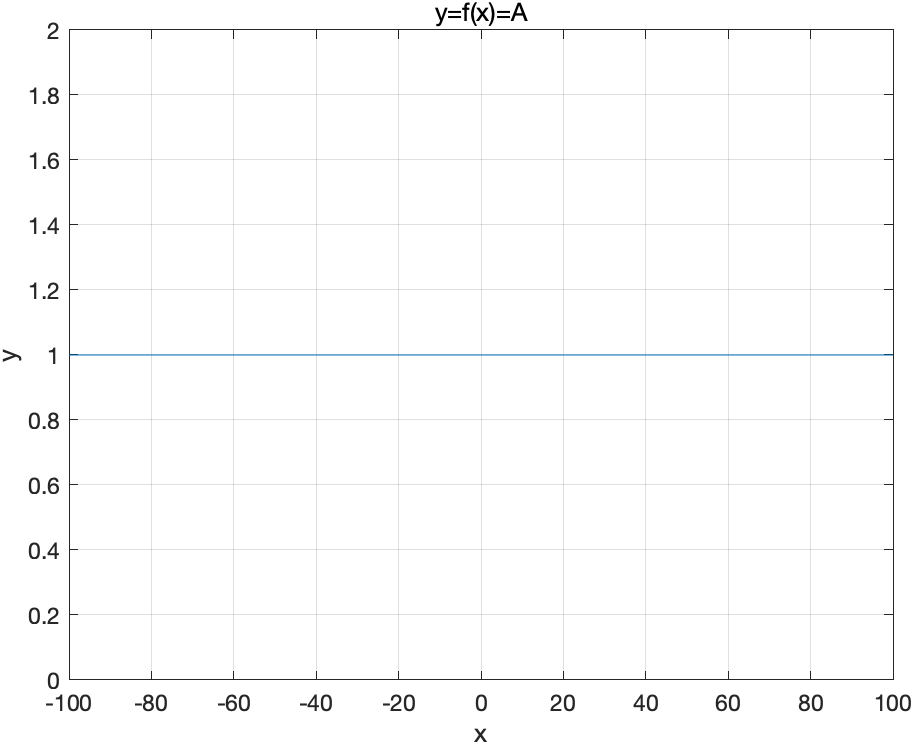
1. $y=A$为偶函数
2. 常用于找交点个数

幂函数

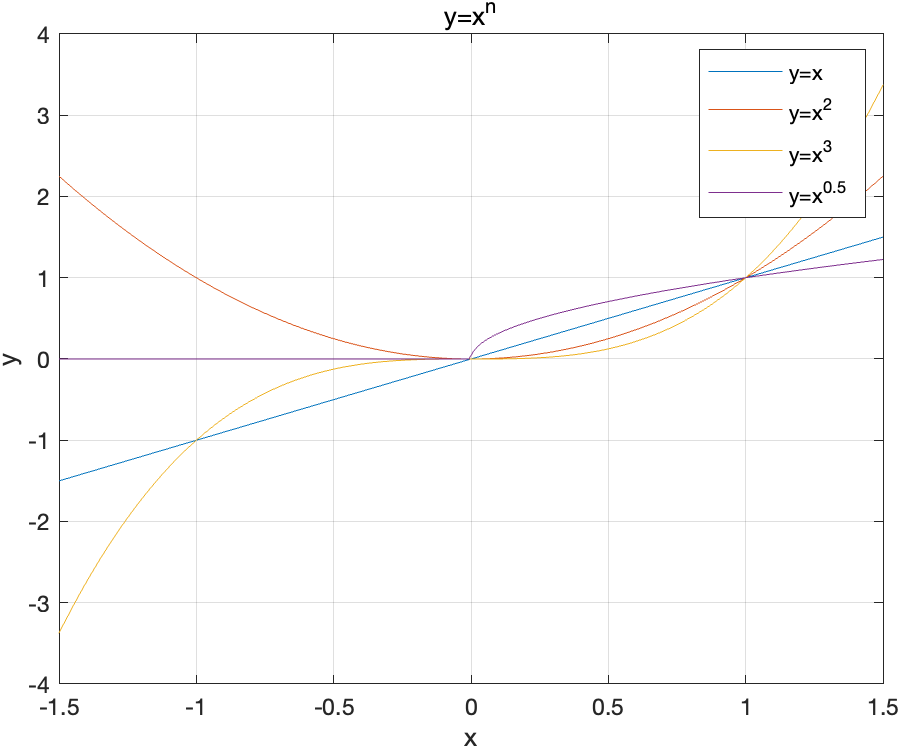
1. 当$y>0$时，$y=x$与$y=\sqrt{x}$、$y=x^{\frac{1}{3}}$、$\ln{x}$有相同单调性，与$y=\frac{1}{x}$有相反的单调性，因此
   1. 见到$y=\sqrt{u}$、$y=u^{\frac{1}{3}}$，可以用$u$来研究最值
   2. $|u|$的最值，直接$|u|=\sqrt{u^2}$，求$u^2$最值即可
   3. $u_1u_2u_3$最值，可以用$\ln{u_1u_2u_3}=\ln{u_1}+\ln{u_2}+\ln{u_3}$
   4. $\frac{1}{u}$最值，看$u$即可（最大最小值相反

指数函数

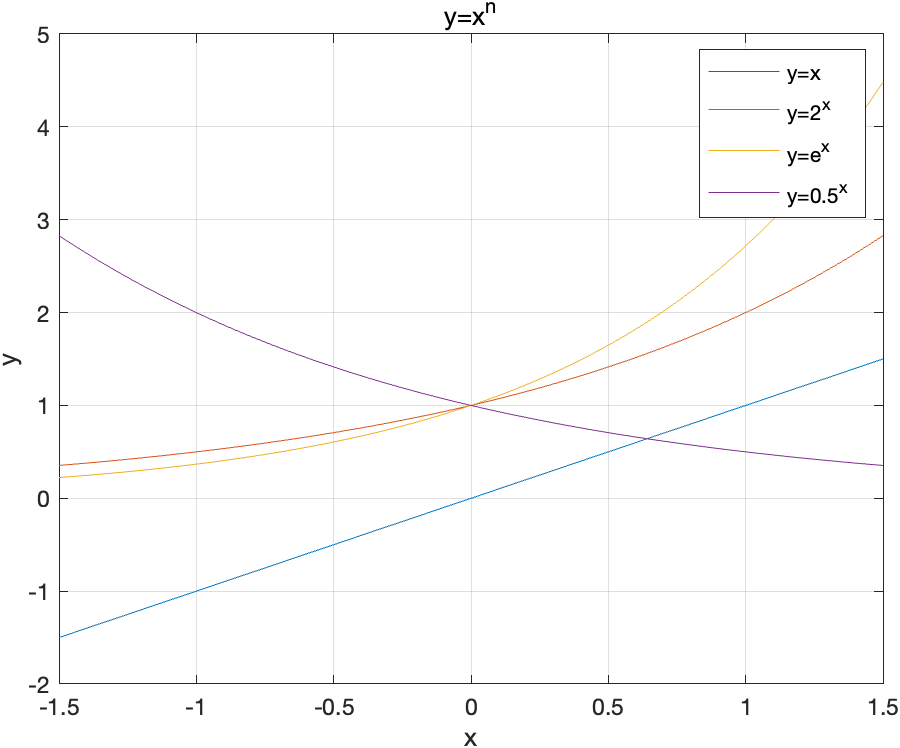
1. $lim_{x\rightarrow{\infty}}e^x$不存在
2. 常用面积：$\int_{-\infty}^0e^xdx=1$

对数函数

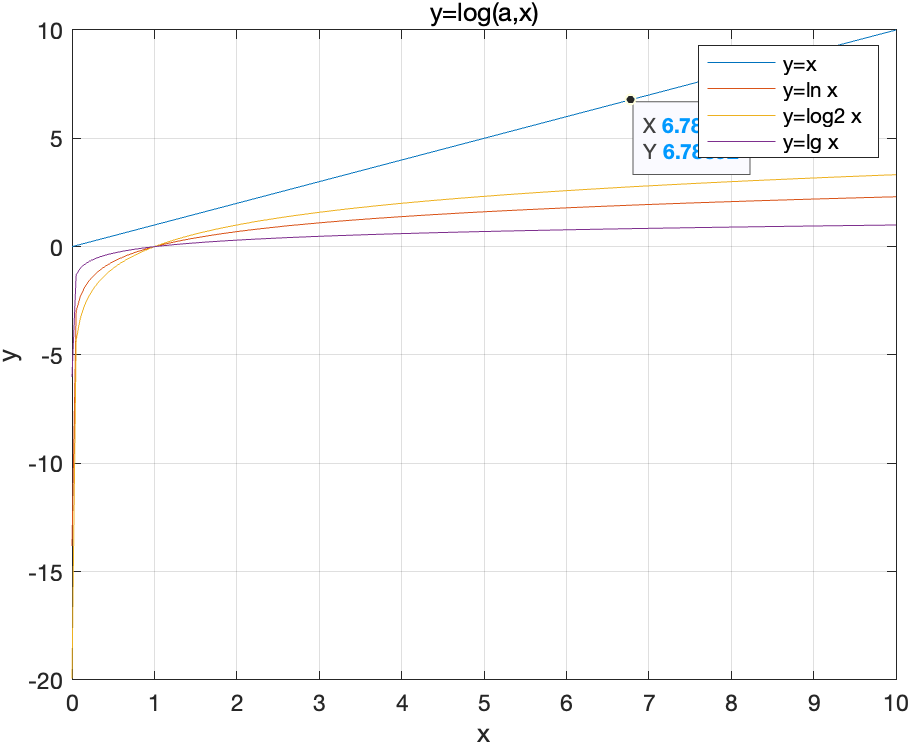
1. 幂指函数$u^v = e^{v\ln{u}}$

三角函数

1. 正弦余弦一拱的面积为2，$\int_0^{\pi}\sin{x}dx=2$
2. $\int_{\frac{\pi}{4}}^\frac{3\pi}{4}\sin{x}dx=\sqrt{2}$
3. $x\rightarrow{0_+}$，$\sin{x}<x$
4. 正割函数$\sec{x} = \frac{1}{\cos{x}}$
5. 余割函数$\csc{x} = \frac{1}{\sin{x}}$
6. 反正弦、反余弦函数
   1. $\arcsin{x}+\arccos{x}=\frac{\pi}{2}$
7. 反正切、反余切
   1. $\lim_{x\rightarrow{+\infty}}\arctan{x}=\frac{\pi}{2}$
   2. $\lim_{x\rightarrow{-\infty}}\arctan{x}=-\frac{\pi}{2}$
   3. $\lim_{x\rightarrow{+\infty}}\arctg{x}=0$
   4. $\lim_{x\rightarrow{-\infty}}\arctg{x}=\pi$
   5. $\arctan{x}+\arcctg{x}=\frac{\pi}{2}$

证明第6点：函数为常数C的一般方法
1. 求导f'(x) = 0  拉格朗日
2. 代值f(x0) = C

图像变换

1. 平移变换
   1. 左增右减
   2. 上下平移
2. 对称变换
   1. $y=-f(x)$，$x$轴对称
   2. $y=f(-x)$，$y$轴对称
   3. $y=-f(-x)$，原点对称
   4. 反函数$y=f^{-1}(x)$关于直线$y=x$对称
   5. 绝对值
      1. $y=|f(x)|$，下边转到上
      2. $y=f(|x|)$，右边转到左。为偶函数
3. 伸缩变换
   1. 水平 $y=f(kx)$
   2. 垂直 $y=kf(x)$

极坐标系下图像

描点法

1. 心形线 $r=a(1-\cos{\theta}),a>0$

1. 三叶玫瑰线 $r=a\sin{3\theta}$

1. 阿基米德螺线 $r=a\theta$

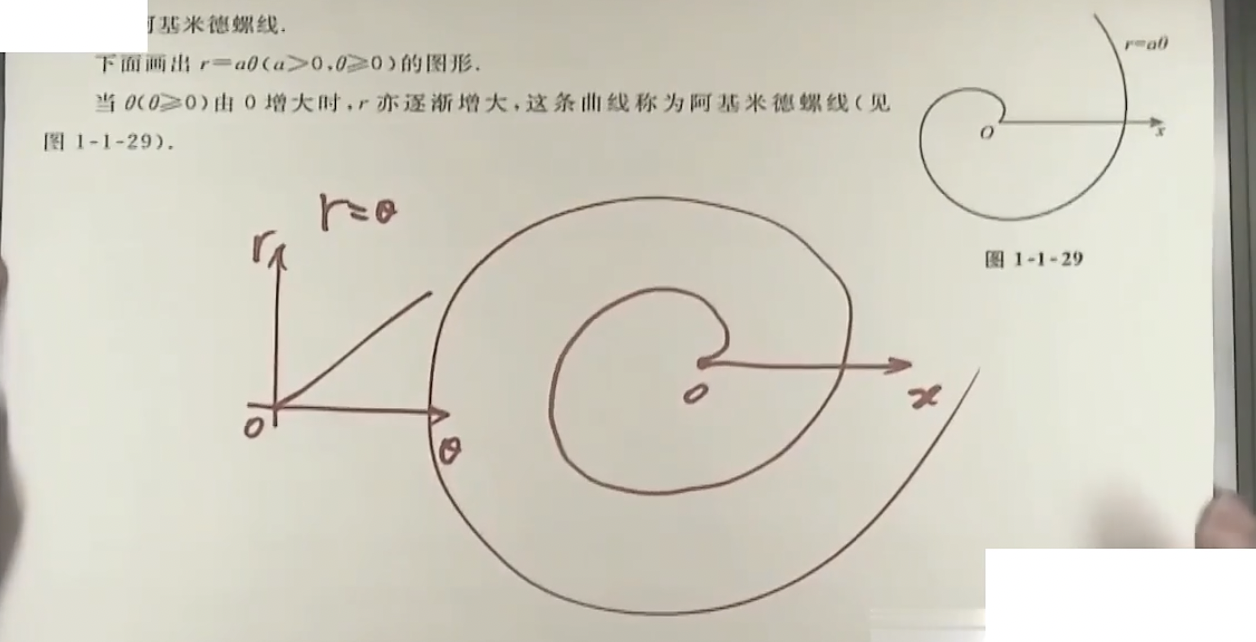
1. 伯努利双纽线 $r^2=a^2\cos{2\theta}$, $r^2=a^2\sin{2\theta}$

直角系观点画极坐标系图像

1. 画直角坐标系下$r$$\theta$图
2. 对应到极坐标系下

赏

谢谢你请我吃糖果

支付宝

微信