leetcode 1706. 球会落何处

2022-02-24

题目

思路

观察到数据量比较小，因此直接模拟就好

难度：Medium
技能：模拟

代码

class Solution {
public:
    vector<int> findBall(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<int> ans(m, -1);
        for(int j=0;j<m;++j){
            int col = j;    // 球在哪一列
            for(auto& row : grid){
                int direction = row[col];
                col += direction;   // 向下滚
                if(col<0 || col>=m ||row[col]!=direction){
                    col = -1;
                    break;
                }
            }
            if(col>=0)  ans[j] = col;
        }
        return ans;
    }
};

展开全文 >>

leetcode 917. 仅仅反转字母

2022-02-23

展开全文 >>

函数与极限

2022-02-21

常用基础知识

数列

等差数列：$a_1,a_2+d,..,a_n+(n-1)d$
1. 通项公式：$a_n = a_1+(n-1)d$
2. $S_n=\frac{n}{2}(a_1+a_n)$
等比数列：$a_1,a_1r,a_1r^2,…,a_1r^{n-1}$
1. 通项公式：$a_n=a_1r^{n-1}$
2. $S_n=na_1(r=1), S_n=\frac{a_1(1-r^2)}{1-r}$
3. 若$|r|<1$,则$\sum_{n=1}^{\infty}r^{n-1}=lim_{x\rightarrow{\infty}}\frac{1-r^n}{1-r}=\frac{1}{1-r}$
常见数列前n项和
1. $\sum_{k=1}^{n}k=1+2+3…+n=\frac{n(n+1)}{2}$
2. $\sum_{k=1}^{n}k^2=\frac{n(n+1)(2n+1)}{6}$
3. $\sum_{k=1}^{n}\frac{1}{k(k+1)}=\frac{1}{12}+\frac{1}{23}+…+\frac{1}{n(n+1)}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1}=\frac{n}{n+1}$

三角函数

三角函数基本关系

$\csc{x}=\frac{1}{\sin{x}}$, $\sec{x}=\frac{1}{\cos{x}}$
$\cot{x}=\frac{1}{\tan{x}}$, $\tan{x}=\frac{\sin{x}}{\cos{x}}$, $\cot{x}=\frac{\cos{x}}{\sin{x}}$
$\sin^2{x}+\cos^2{x}=1$, $1+\tan^2{x}=\sec^2{x}$, $1+\cot^2{x}=\csc^2{x}$

诱导公式：奇变偶不变，符号看象限(原函数)

角度	$\frac{\pi}{2}-\alpha$	$\frac{\pi}{2}+\alpha$	$\pi-\alpha$	$\pi+\alpha$	$\frac{3\pi}{2}-\alpha$	$\frac{3\pi}{2}+\alpha$	$2\pi-\alpha$
$\sin{\theta}$	$\cos{a}$	$\cos{a}$	$\sin{a}$	$-\sin{a}$	$-\cos{a}$	$-\cos{a}$	$-\sin{a}$
$\cos{\theta}$	$\sin{a}$	$-\sin{a}$	$-\cos{a}$	$-\cos{a}$	$-\sin{a}$	$\sin{a}$	$\cos{a}$
$\tan{\theta}$	$\cot{a}$	$-\cot{a}$	$-\tan{a}$	$\tan{a}$	$\cot{a}$	$-\cot{a}$	$-\tan{a}$
$\cot{\theta}$	$\tan{a}$	$-\tan{a}$	$-\cot{a}$	$\cot{a}$	$\tan{a}$	$-\tan{a}$	$-\cot{a}$

倍角公式

$\sin{2a}=2\sin{a}\cos{a}$
$\cos{2a}=\cos^2{a}-\sin^2{a}=2\cos^2{a}-1=1-2\sin^2{a}$
$\tan{2a}=\frac{2\tan{a}}{1-\tan^2{a}}$
$\cot{2a}=\frac{\cot^2{a}-1}{2\cot{a}}$
$\sin{3a}=-4\sin^3{a}+3\sin{a}$
$\cos{3a}=4\cos^3{a}-3\cos{a}$

半角公式

$\sin^2{\frac{a}{2}}=\frac{1}{2}(1-\cos{a})$
$\cos^2{\frac{a}{2}}=\frac{1}{2}(1+\cos{a}$)

和差公式

$\sin(a\pm{b})=\sin{a}\cos{b}\pm \cos{a}\sin{b}$
$\cos({a\pm b})=\cos{a}\cos{b}\mp \sin{a}\sin{b}$
$\tan({a\pm b})=\frac{\tan{a}\pm \tan{b}}{1 \mp \tan{a}\tan{b}}$, $\tan{(\frac{\pi}{4}-x)}=\frac{1-\tan{x}}{1+\tan{x}}$

和差化积

$\sin{a}+\sin{b}=2\sin{\frac{a+b}{2}}\cos{\frac{a-b}{2}}$
$\sin{a}-\sin{b}=2\sin{\frac{a-b}{2}}\cos{\frac{a+b}{2}}$
$\cos{a}+\cos{b}=2\cos{\frac{a+b}{2}}\cos{\frac{a-b}{2}}$
$\cos{a}-\cos{b}=-2\sin{\frac{a+b}{2}}\sin{\frac{a-b}{2}}$

积化和差

$\sin{a}\cos{a}=\frac{1}{2}[\sin{(a+b)}+\sin{(a-b)}]$
$\cos{a}\sin{a}=\frac{1}{2}[\sin{(a+b)}-\sin{(a-b)}]$
$\cos{a}\cos{a}=\frac{1}{2}[\cos{(a+b)}+\cos{(a-b)}]$
$\sin{a}\sin{a}=\frac{1}{2}[\cos{(a-b)}-\cos{(a+b)}]$

指数运算

$a^\alpha ·a^\beta=a^{\alpha+\beta}$
$\frac{a^\alpha}{a^\beta}=a^{\alpha-\beta}$
$(a^\alpha)^{\beta}=a^{\alpha\beta}$
$(ab)^\alpha=a^{\alpha}·b^{\alpha}$
$(\frac{a}{b})^\alpha=\frac{a^\alpha}{b^\alpha}$

对数运算法则

$log_a(MN)=log_aM+log_aN$
$log_a(\frac{M}{N})=log_aM-log_aN$
$log_aM^N=Nlog_aM$

方便求导

$\ln{\sqrt{x}}=\frac{1}{2}\ln{x}$
$\ln{\frac{1}{x}}=-\ln{x}$
$\ln{(1+\frac{1}{x})}=\ln{\frac{x+1}{x}}=\ln{(x+1)}-\ln{x}$

一元二次方程基础

形式：$ax^2+bx+c=0,(a\neq0)$
根的公式：$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$
韦达定理：$x_1+x_2=-\frac{b}{a}$, $x_1x_2=\frac{c}{a}$
判别式：$\Delta=b^2-4ac$：$\Delta>0$两个不等实根；$\Delta=0$一个实根；$\Delta<0$两个共轭复根
抛物线$y=ax^2+bx+c$的顶点为$(-\frac{b}{2a},c-\frac{b^2}{4a})$

因式分解

$(a+b)^2=a^b+2ab+b^2$, $(a-b)^2=a^2-2ab+b^2$
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$, $(a-b)^3=a^3-3a^2b+3ab^2-b^3$
$a^2-b^2=(a+b)(a-b)$
$a^3-b^3=(a-b)(a^2+ab+b^2)$, $a^3+b^3=(a+b)(a^2-ab+b^2)$
二项式定理：$(a+b)^n=\sum_{k=0}^nC_n^ka^{n-k}b^k$
- $C_n^k=\frac{n!}{k!(n-k)!}$，就是杨辉三角

阶乘与双阶乘

$n!=1·2·3·…·n$
- 规定$0!=1$
$(2n)!!=2·4·6·…·(2n)=2^n·n!$
$(2n-1)!!=1·3·5·…·(2n-1)$
华里士公式（其中就包含双阶乘
- $\int_0^{\frac{\pi}{2}}\sin^n{x}dx=\frac{n}{n-1}\frac{n-2}{n-3}…1,(n为奇数)$
- $\int_0^{\frac{\pi}{2}}\sin^n{x}dx=\frac{n}{n-1}\frac{n-2}{n-3}…\frac{1}{2}\frac{\pi}{2},(n为偶数)$
- $\int_0^{\frac{\pi}{2}}\cos^n{x}dx=\frac{n}{n-1}\frac{n-2}{n-3}…1,(n为奇数)$
- $\int_0^{\frac{\pi}{2}}\cos^n{x}dx=\frac{n}{n-1}\frac{n-2}{n-3}…\frac{1}{2}\frac{\pi}{2},(n为偶数)$

常用不等式

$|a\pm b|\le |a|+|b|$
- $|a_1\pm a_2\pm a_3 \pm …\pm a_n|\le |a_1|+|a_2|+…|a_n|$
- $|\int_a^bf(x)dx|\le \int_a^b|f(x)|dx$
$|a|-|b|\le |a-b|$
$||a|-|b||\le{|a-b|}$
$\sqrt{ab}\le{\frac{a+b}{2}\le{\sqrt{\frac{a^2+b^2}{2}}}}$
$|ab|\le{\frac{a^2+b^2}{2}}$
$\sin{x}<x<\tan{x}, 0<x<\frac{\pi}{2}$
$\arctan{x}\le{x}\le{\arcsin{x}},0\le{x}\le{1}$
$\sin{x}\le{x},\forall{x}$
- $X_{n+1}=\sin{X_n}$，由$X_{n+1}=\sin{X_n}\le{X_n}$，$X_n$单调减少
$e^x\ge{x+1},\forall{x}$
- $X_{n+1}=e^{X_n}-1$，由$X_{n+1}=e^{X_n}-1\ge{X_n}$，$X_n$单调增加
$x-1\ge{\ln{x}},x>0$
- $X_{n+1}=\ln{X_n}+1$，由$X_{n+1}=\ln{X_n}+1\le{X_n}$，$X_n$单调减少
$\frac{1}{1+x}<\ln{(1+\frac{1}{x})}<\frac{1}{x}$
- 拉格朗日中值定理可以证明

#

反双曲正弦

1.1 函数

一些定义

概念

x，y为两个变量，x ∈ D，如果 x ∈ D，总存在唯一确定的y与x对应，称y为x的函数，记作 y = f(x)

D 称为定义域

R = {y| y = f(x), x ∈ D} 称为函数的值域

∀ 表示任意
∃ 表示存在

特殊的函数

符号函数

sgn x = -1, x < 0; 0, x = 0; 1, x > 0

迪利克雷函数

D(x) = 1, x ∈ Q （有理数）; 0, x ∈ R\Q

取整函数向下取整

y = [x]

反函数

若函数 y=f(x) 严格单调，记 x=g(y) 为f的反函数

严格单调函数必有反函数（积分换元法需要使用）；有反函数的函数不一定单调
$y=f(x)$和$x=f^{-1}(y)$在同一坐标系中的图像完全重合
$y=f(x)$和$y=f^{-1}(x)$在同一坐标系中的图像关于$y=x$对称，这是$x$和$y$互换的结果

复合函数

函数$y=f(u)$定义域为$D_f$，函数$u=g(x)$定义域为$D_g$且$g(D_g)\in{D_f}$，则$y=f[g(x)],x\in{D_g}$确定的函数称为函数$u=g(x)$和$y=f(u)$构成的复合函数

基本初等函数

幂指对三角反三角

x^a
a^x (a>0 && a!=1)
log(a, x)
sinx cosx tanx cotx secx cscx
arcsinx arccosx arctanx arccotx

初等函数

由常数和基本初等函数经过有限次四则运算和复合运算得到的函数

参数方程

摆线
1. 可看作自行车轮子一点滚动形成的轨迹
2. $x=r(t-\sin{t})$, $y=r(1-\cos{t})$

星形线（内摆线
1. 小圆在大圆内部做纯滚动，大圆半径为小圆半径的4倍
2. $x=r\cos^3{t}$, $y=r\sin^3{t}$
3. $x^{\frac{2}{3}}+y^{\frac{2}{3}}=r^{\frac{2}{3}}$

初等函数的性质

奇偶性

D 首先必须关于原点对称！否则就免谈

$f(-x) = f(x)$ 偶函数，函数图像关于$y$轴对称
$f(-x) = -f(x$) 奇函数，函数图像关于原点对称

$F_1(x)=f(x)-f(-x)$必为奇函数
1. 双曲正弦$\sh{x} = \frac{e^x-x^{-x}}{2}$为奇函数
2. 其反函数为反双曲正弦$arsinh(x)=\ln{(x+\sqrt{x^2+1})}$
3. $(\ln{(x+\sqrt{x^2+1})})’=\frac{1}{\sqrt{x^2+1}}$
4. $\int{\frac{1}{\sqrt{x^2+1}}}dx=\ln{(x+\sqrt{x^2+1})}+C$
$F_2(x)=f(x)+f(-x)$必为偶函数
1. 双曲正弦$\ch{x} = \frac{e^x+x^{-x}}{2}$为偶函数
奇函数在原点有定义时，$f(0)=0$
偶函数在原点可导时，$f’(0)=0$
函数关于$x=T$对称的充要条件：$f(x)=f(2T-x)$或者$f(x+T)=f(x-T)$

单调性

y = f(x) x ∈ D

$\forall x_1, x_2 \in D$ 且 $x_1 < x_2$，有 $f(x_1) < f(x_2)$，称$f(x)$在$D$上严格单调递增
∀ x1, x2 ∈ D 且 x1 < x2，有 f(x1) > f(x2)，称f(x)在D上严格单调递减

后期会经常使用求导来讨论函数在某个区间上的单调性
但是定义法也不能忘记，比如离散的数列就不能求导

有界性

$y=f(x),x\in{D}$

∃ M>0，对于 ∀ x ∈ D，有 |f(x)| <= M，称f(x)在D上有界
∃ M1，对于 ∀ x ∈ D，f(x) >= M1，称函数有下界 M1
∃ M2，对于 ∀ x ∈ D，f(x) <= M2，称函数有上界 M2

函数有界的充分必要条件是函数既有上界又有下界

讨论函数有界与否必须首先指明区间$I\in{D}$

周期性

y = f(x) x ∈ D

如果 ∃ T>0，使得 ∀ x ∈ D (x+T ∈ D)，有 f(x+T) = f(x)，称f(x)是具有周期性

对于周期函数$f(x)$，其在一个周期内的积分值与积分起点无关
1. $\int_0^Tf(x)dx=\int_a^{a+T}f(x)d(x)$
2. 可以得知：奇函数在一个周期内的积分值为0

重要结论

若$f(x)$为可导的偶函数，则$f’(x)$为奇函数
若$f(x)$为可导的奇函数，则$f’(x)$为偶函数
若$f(x)$是可导的周期函数，则$f’(x)$也是以$T$为周期的周期函数
连续的奇函数的一切原函数都是偶函数
连续的偶函数的原函数中仅有一个原函数是奇函数（$f(0)=0$
若连续函数$f(x)$以$T$为周期且$\int_0^Tf(x)dx=0$，则$f(x)$的一切原函数也周期$T$
若$f(x)$在$(a,b)$内可导且$f’(x)$有界，则$f(x)$在$(a,b)$有界（拉格朗日证明

1.2 数列极限

定义

$\forall\epsilon>0,\exist{N}>0,n>N$时，恒有$|x_n-a|<\epsilon$，则$\lim_{n\rightarrow{\infty}}x_n=a$

写距离 $|x_n-a|<\epsilon$
反解出$n$的范围$n>g(\epsilon)$
取$N=[g(\epsilon)]+1$

$\lim_{n\rightarrow{\infty}a_n=0}$和$\lim_{n\rightarrow{\infty}｜a_n｜=0}$互为充要条件

性质

唯一性：数列若有极限，该极限唯一

1 2	证明数列极限唯一性取 ℇ = (A - B) / 2

有界性：如果数列有极限，那么数列有界

证明数列极限有界性
取 ℇ = 1
lim(n->∞) an = A, 所以 ∃ N > 0, n > N 时 |an - A| < 1
因为 | |an| - |A| | <= |an - A|
所以 n > N 时，||an| - |A| | < 1

|an| < 1 + |A|  这个式子仅当 n > N 成立
因此若想对全体数列项成立，取 M = max{|a1|,|a2|....|aN|, 1+|A|}
∀ n，有|an| <= M 证毕

有界的数列不一定有极限

1	例如 an = 1 + (-1)^n

保号性：如果 lim(n->∞) an = A，如果A>0（或A<0），则 ∃ n> 0，n > N 时，an>0（或 an<0）

1
2
3

证明数列极限保号性
假设 A>0，取 ℇ = A/2
假设 A<0，取 ℇ = -A/2

如果{$a_n$}收敛，则其任何子列{$a_{n_k}$都收敛，且极限相等}

1.3 函数极限

定义

x->a
∀ ℇ>0，∃ 𝞭>0，当 0<|x-a|<𝞭，|f(x)-A|<ℇ，称f(x)当x->a时的极限为A
记作 lim(x->a) f(x) = A

x->a的过程中，x不取到a，因此极限是否存在与f(x)在a点有无定义没有关系
x->a包含 x->a- 和 x->a+ 包含左极限和右极限
函数在a点极限存在的充要条件是：在a点的左极限右极限存在且相等 f(a+0) = f(a-0)

考点

用定义证明函数极限
给分段函数，根据左右极限求一些系数

x->+∞
∀ ℇ>0, ∃ X>0, x>X时, |f(x)-A| < ℇ 称lim(x->+∞) f(x) = A
x->-∞
∀ ℇ>0, ∃ X>0, x<-X时, |f(x)-A| < ℇ 称lim(x->-∞) f(x) = A
x->∞
∀ ℇ>0, ∃ X>0, |x|>X时, |f(x)-A| < ℇ 称lim(x->∞) f(x) = A

性质

唯一性：函数有极限，极限必定唯一

1
2
3

证明唯一性：
反证：取 ℇ = (A-B)/2 > 0
可以根据定义，发现矛盾

$\lim_{x\rightarrow{+\infty}}e^x=+\infty, \lim_{x\rightarrow{-\infty}}e^x=0$, 故$\lim_{x\rightarrow{\infty}}e^x$不存在
$\lim_{x\rightarrow{0}}\frac{\sin{x}}{|x|}$不存在
$\lim_{x\rightarrow{0}}\arctan{x}$不存在
$\lim_{x\rightarrow{0}}[x]$不存在

局部有界性：lim(x->a) f(x) = A, 则 ∃ 𝞭>0，M>0，0<|x-a|<𝞭 时|f(x)|<=M

1
2
3

证明唯一性：
反证：取 ℇ = 1
可以根据定义证明出

保号性：lim(x->a) f(x) = A，A>0（或者A<0），则 ∃ 𝞭>0，当 0<|x-a|<𝞭时，f(x)>0（或者f(x)<0）

取 ℇ = A/2

1.4 无穷小和无穷大

无穷小

a(x)为x的函数，如果lim(x->x0) a(x) = 0，则称a(x)当x->x0时为无穷小

0是无穷小，但无穷小不一定是0
对于a(x)!=0，a(x)是否为无穷小与自变量的趋向有关

等价定义：∀ ℇ>0, ∃ 𝞭>0,当 0<|x-x0|<𝞭时，|a(x)-0|<ℇ 即 lim(x->x0) a(x) = 0

一些性质：

两个无穷小的和差仍为无穷小
常数与无穷小之积仍为无穷小
多个无穷小之积仍为无穷小
lim(x->x0) f(x) = A 的充分必要条件是：f(x)=A+a, a->0 (x->x0)

无穷大

∀ M>0, ∃ 𝞭>0, 当0<|x-x0|<𝞭, 有|f(x)|>M, 称f(x)当x->x0时为无穷大，记作lim(x->x0) f(x) = ∞
∀ M>0, ∃ X>0, 当x>|X|, 有|f(x)|>M, 称f(x)当x->∞时为无穷大，记作lim(x->∞) f(x) = ∞

无穷小和无穷大的关系

lim(x->x0) f(x) = 0 ==> lim(x->x0) 1/f(x) = ∞

1.5 极限的运算法则

预备知识：初等函数无穷小

四则运算法则

条件：x->x0, f(x0)->A, g(x)->B

x->x0时，f(x)+g(x)->A+B, f(x)-g(x)->A-B

1	f(x) = A+a, g(x) = B+b 易证明

k为常数，lim(x->x0) kf(x) = kA

lim(x->x0) f(x)g(x) = AB

如果lim(x->x0) g(x) != 0，则lim(x->x0) f(x)/g(x) = A/B

多项式除法的极限，同除以最高次项（或最低次项

复合运算极限法则

嵌套

1.6 极限存在准则包括两个重要极限

I.夹逼定理

数列的情形

an <= bn <= cn
lim(n->∞) an = lim(n->∞) cn = A
那么，lim(n->∞) bn = A

函数的情形

f(x) <= g(x) <= h(x)
lim f(x) = lim h(x) = A
那么，lim g(x) = A

如果$\phi{(x)}\le{f(x)}\le{g(x)}$且$\lim[g(x)-\phi(x)]=0$，$\lim{f(x)}$也不一定存在

II.单调有界数列必定有极限

{an} 有界的充要条件是 {an} 有上下界
如果 {an} 单调递增，那么一定有下界。极限是否存在取决于是否有上界
如果 {an} 单调递减，那么一定有上界。极限是否存在取决于是否有下界

两个重要极限

lim(x->0) six/x = 1
推广：lim(∆->0) (sin∆)/∆ = 1

lim(n->∞) (1+1/n)^n = e
推广 lim(n->0) (1+n)^(1/n) = e
lime(∆->0) (1+1/∆)^∆ = e

(1^∞) 类型的极限，一般都要往第二个重要极限凑

1.7 无穷小的比较

有界函数乘以无穷小仍为无穷小

设 a->0 b->0

lim (a/b) = 0, 称a为b的高阶无穷小，记作 a=o(b)
lim (a/b) = ∞, 称a为b的低阶无穷小
lim (a/b) = k, k为常数，称a和b为同阶无穷小，如果 k=1, 那么a和b为等价无穷小 a~b
lim (a/b^k) = K, 称a为b的k阶无穷小

等价无穷小的性质

a->0, b->0, 则 a~b 的充分必要条件是 b = a + o(a)（高阶）

a~a1, b->b1, lim(b1/a1) = A, 那么 lim(b/a) = A。这意味着求极限可以等价无穷小替换

$o(x^m)\pm o(x^n)=o(x^l), l=\min(m,n)$
$o(x^m)o(x^n)=o(x^{m+n})$
$o(x^m)=o(kx^m)=ko(x^m),k=C$

常见等价无穷小

以下趋势均为 x->0

x ~ sin(x)
x ~ tan(x)
x ~ arcsin(x)
x ~ arctan(x)
x ~ ln(1+x)
x ~ e^x-1
$a^x-1$~$x\ln{x}$
1-cosx ~ x^2/2
(1+x)^a-1 ~ ax

1.8 函数的连续性和间断点

f(x)在某一点连续连续

若$\lim_{x\rightarrow{x_0}}f(x)=f(x_0)$

f(a-0)=f(a)称f(x)在x=a左连续；f(a+0)=f(a)右连续
f(x)在x=a连续的充要条件是f(x)在x=a左连续，右连续

f(x)在闭区间连续

若f(x)在[a,b]上有定义，f(x)在(a,b)内处处连续，f(a)=f(a+0),f(b)=f(b-0)，那么称f(x)在[a,b]上连续
记作 f(x) ∈ C[a,b]

间断点及分类

在点$x_0$的某去心领域内有定义的前提下才讨论间断点
lim(x->a) f(x) != f(a)，称f(a)在x=a间断

间断点的分类：

第一类间断点：f(a-0)和f(a+0)都存在
1. 可去间断点：f(a-0)=f(a+0)
2. 跳跃间断点：f(a-0)!=f(a+0)
第二类间断点：f(a-0)和f(a+0)至少一个不存在
1. 无穷间断点：$\lim_{x\rightarrow{x_0}}f(x)=\infty$
2. 振荡间断点
3. 其他

1.9 连续函数的运算和初等函数连续性

连续函数的运算

四则运算

f(x) g(x) 在x=x0连续，则f(x)+g(x)和f(x)-g(x)和f(x)g(x)在x=x0连续
若g(x0)!=0, 则f(x)/g(x)在x=x0连续

复合运算

复合函数的连续性可以得到保持

初等函数连续性

复习一下，基本初等函数：幂指对三角反三角

初等函数：常数和基本初等函数经过有限次复合和四则运算得到的函数

基本初等函数在其定义域内连续
初等函数在其定义域内连续

1.10 闭区间上连续函数的性质

最值定理：f(x)∈C[a,b],则f(x)在[a,b]取得到最小值m和最大值M
有界定理：若f(x)∈C[a,b]，则∃k>0，使∀x∈[a,b]，有|f(x)|<=k
零点定理：若f(x)∈C[a,b]，f(a)·f(b)<0, 则必定存在x0∈[a,b],f(x0)=0
介值定理：若f(x)∈C[a,b]，则∀n∈[m,M], 则∃𝝽∈[a,b]使得f(𝝽)=n
即介于m和M的任意值都可以被取到

TIPS：

函数闭区间连续，证明开区间问题，首选零点定理
函数闭区间连续，证明闭区间问题 / 函数值之和，选介值定理

补充

海涅定理

设f(x)在$\hat{U}(x_0,\delta)$有定义，则
$\lim_{x\rightarrow{x_0}}f(x)=A$存在的充要条件是
对任何$\hat{U}(x_0,\delta)$内，以$x_0$为极限的数列{$x_n$}，极限$\lim_{n\rightarrow{\infty}}f(x_n)=A$存在

从右往左推：取两个不同的数列{$x_n$}，否定函数极限的存在
从左到右推：$\lim_{x\rightarrow{x_0}}f(x)=A => \lim_{n\rightarrow{\infty}}f(x_n)=A$

七种未定式极限

$\frac{0}{0}, \frac{\infty}{\infty}, 0·\infty$
$\infty - \infty$
$\infty^0, 0^0, 1^\infty$

遇到根号，有理化
等价无穷小
泰勒展开
取整函数相关的，用$x-1<[x]\le{x}$，夹逼定理
$\infty-\infty$，有分母则通分，没有则创造分母（换元$x=\frac{1}{t}$
幂指函数化为$e^{v\ln{u}}$
$1^{\infty}$：$\lim{u^v}=e^{\lim{v\ln{u}}}=e^{\lim{v(u-1)}}$
海涅定理

展开全文 >>

leetcode 838. 推多米诺

2022-02-21

这里做题

一图流

展开全文 >>

数制和计算

2022-02-19

2.1.1 进位计数制

十进制计数法：

Kn,Kn-1,Kn-2,…,K0,K-1,K-2,…,K-m = SIGMA (i=-m ~ n) [Ki * 10^(i-1)]

二进制： 0 1

八进制： 0 1 2 3 4 5 6 7

十六进制 0 1 2 3 4 5 6 7 8 9 A B C D E F

真值机器数

进制转换

r进制转换为十进制：所有数值乘以各自位权之和
二进制转八进制：三位为一组
二进制转十六进制：四位为一组
十进制转r进制
- 整数部分：除以r取余数，逆序
- 小数部分：乘以r取整，正序可能会有精度损失

2.1.2 BCD码

4个bit表示1个十进制字符

8421码

就是二进制 8421分别为位权。有6种冗余

985 = 1001,1000,0101

为了避免冗余状态的出现，进行加法可能需要+6进一位，进行减法可能需要-6

1
2
3

例如
  5  +   8   = 13
0101 + 1000  = 1101 + 0110 = 1 0011

余3码

8421基础上+3

每一位数没有固定的权值，属于是无权码

2421码

权值分别是 2 4 2 1

为了不发生歧义，规定0-4的2421码第一位为0，5-9的第一位为1

字符和字符串

ASCII码

32～126 可印刷字符其余为控制、通信字符

0~9 48（0011 0000）～ 57（0011 1001）：高4位相同，低四位为8421码

A~Z 65～90

a~z 97～122

汉字的表示和编码

GB 2312-80

包含区位码和位数据传输可能出现问题（可能理解为ASCII的0-31

因此，区位码和位码都加上20H，得到国标码，可以避免和控制/通信字符冲突

汉字内码 = 国标码+80H

大小端

大端：多字节数据的高字节放在低地址

小端：多字节数据的低字节放在低地址

2.1.4 奇偶校验码

校验原理

码字：若干位代码组成的一个字称为码字
两个码字间的距离：两个码字逐位进行对比，不同的位的个数
一种编码方案可能有若干个合法码字，各合法码字之间的最小距离称为码距

例如编码：00 01 10 11 都是合法码字（码距为1），那么发生位错误时，就会被认为是另一个合法码字

如果增加一位校验位，编码：100 001 010 111，3bit映射到4个合法状态（码距位2），发生1bit错误时，就可以检验出来

奇偶校验码

奇校验码：整个校验码中，“1”的个数为奇数

偶校验码：整个校验码中，“1”的个数位偶数

假定最高位设置校验位

1001101 奇校验码：1,1001101 偶校验码：0,1001101
1010111 奇校验码：0,1010111 偶校验码：1,1010111

检错：用一种校验方案，发送方和接收方检验1的个数奇偶性

偶校验的硬件实现

各个信息位进行模2加运算，得到的结果就是偶校验位

模2加
0^0 = 0
1^1 = 0
1^0 = 1
0^1 = 1

偶数个1异或会变成0，若干个0异或还是0，而偶校验位也应该是0，

校验：所有位进行异或运算，结果为1说明出错

2.1.5 海明校验码

思想：多位校验位，可以携带对错信息，以及错误位置。实现检查、纠正错误

假设有n位信息位，k位校验位，k需要多少才行呢？
n+k位码，每一位都可能出错，k位可以携带2^k信息，所以
2^k >= n+k+1 才可以 1代表正确的

2^k >= n+k+1

校验位的分布：校验位Pi放在海明码中2^(i-1)的位置，下标从1开始

海明码求解步骤

海明码纠错

校验位和分组内的信息位进行异或

补充

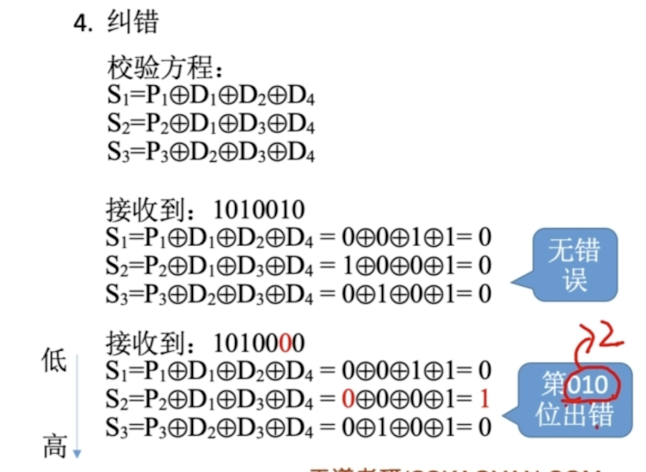
海明码具有1位纠错能力，2位检错能力

2.1.6 循环冗余校验码 CRC

思想：数据的发送方和接受方约定一个“除数”

K个信息位+R个校验位作为“被除数”，添加校验位后需要保证除法的余数为0

2.2.1 定点数的表示

无符号数

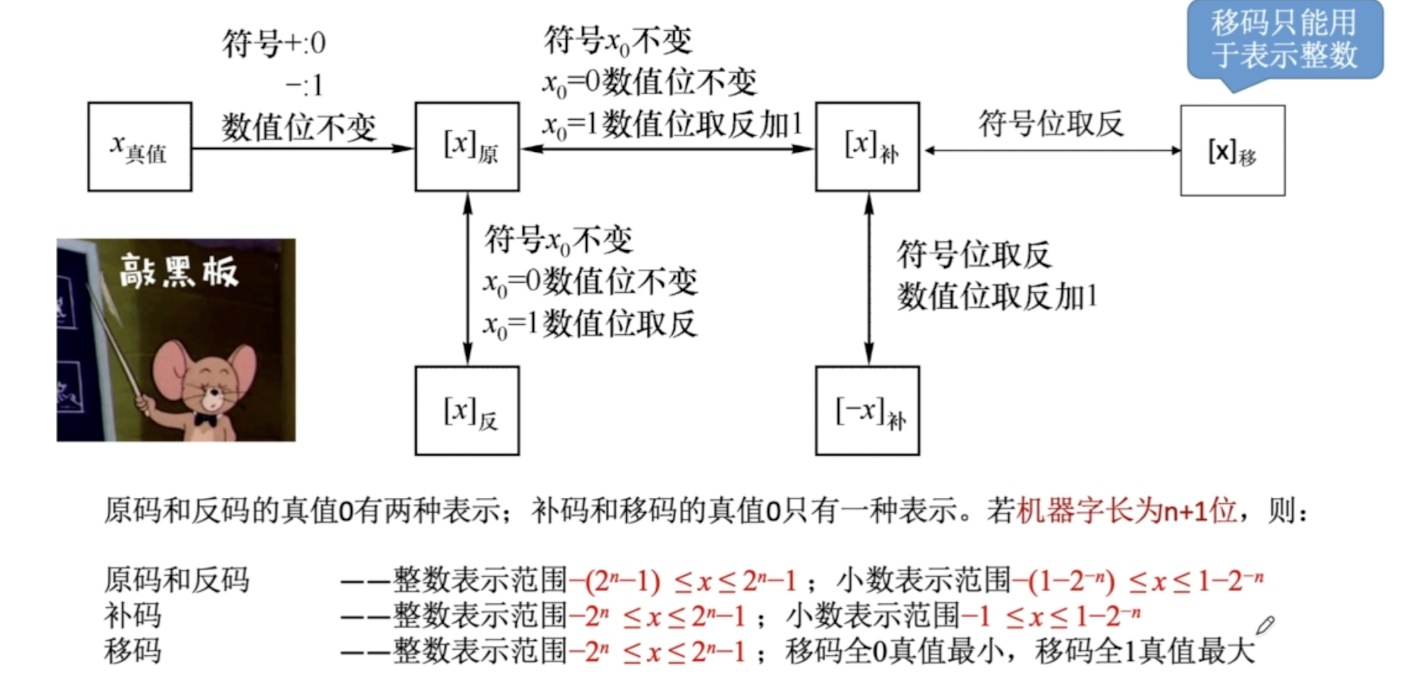
通常只讨论无符号整数而不考虑无符号小数

整个机器字长的全部二进制位都是数值位，没有符号位，相当于绝对值

表示范围：0 ~ 2^n-1

有符号数的定点表示

定点整数：小数点位置隐含在最后，最高位为符号位

定点小数：小数点隐含在最高位后面，最高位为符号位

原码

尾数表示真值的绝对值，符号位 0/1 对应正/负

机器字长n+1位的原码整数可以表示的范围是： -(2^n-1) ~ (2^n-1)

机器字长n+1位的原码小数可以表示的范围是： -(1-2^(-n)) ~ (1-2^(-n))

真值0有+0和-0两种形式

反码

正数的反码：和原码相同

负数的反码：符号位不变，数值位全部取反

由于和原码一一对应，所以他俩的表示范围也相同

补码

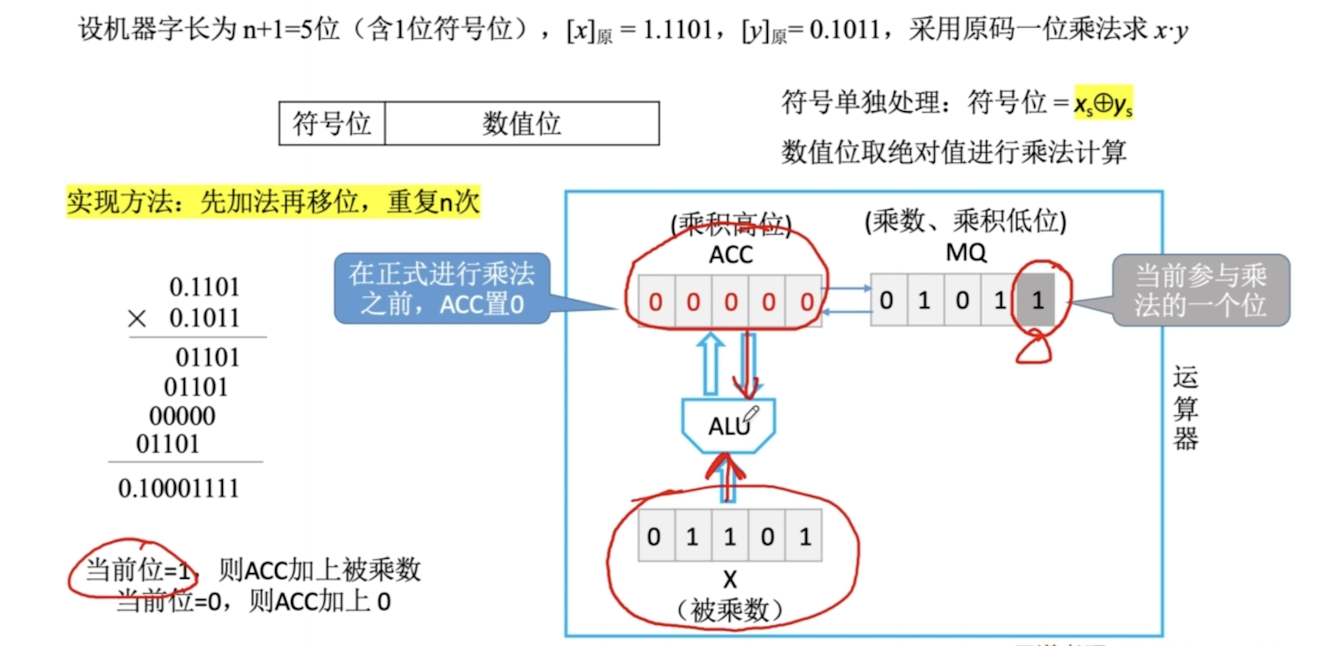
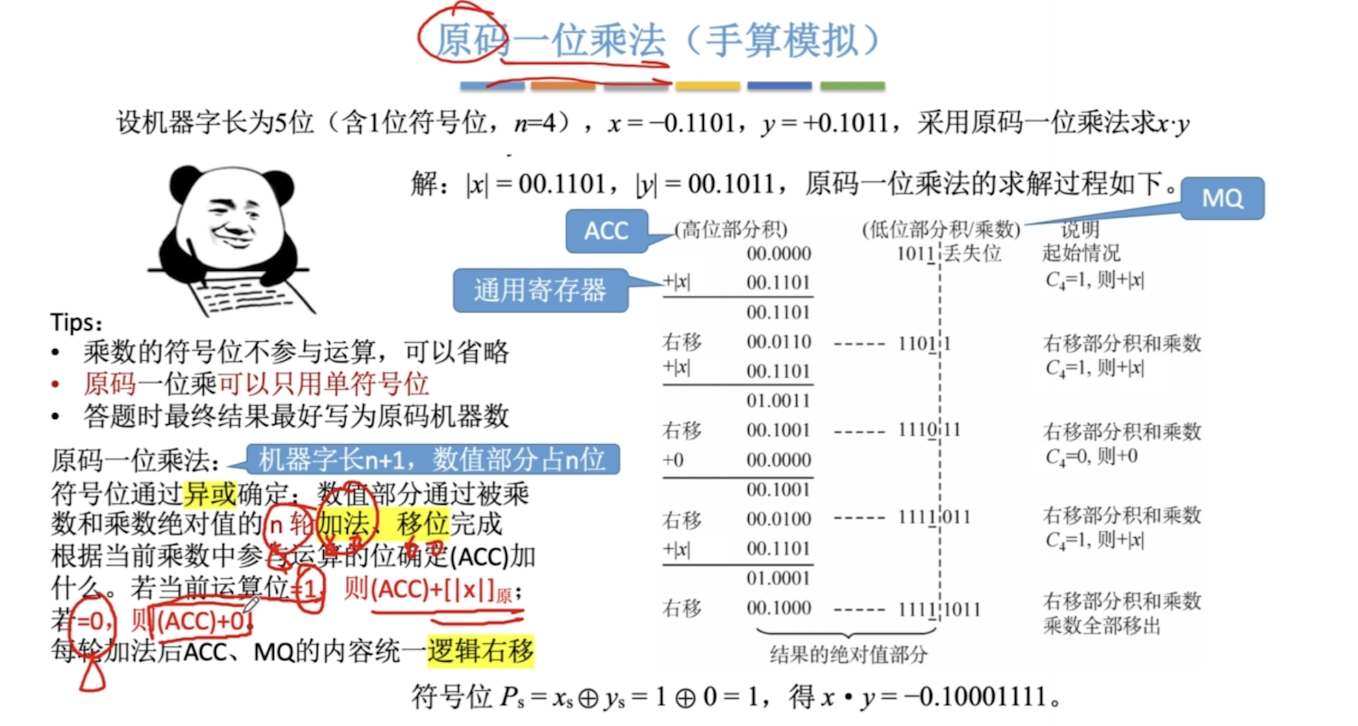
可以用加法替代减法，符号位参与运算，减少硬件开销

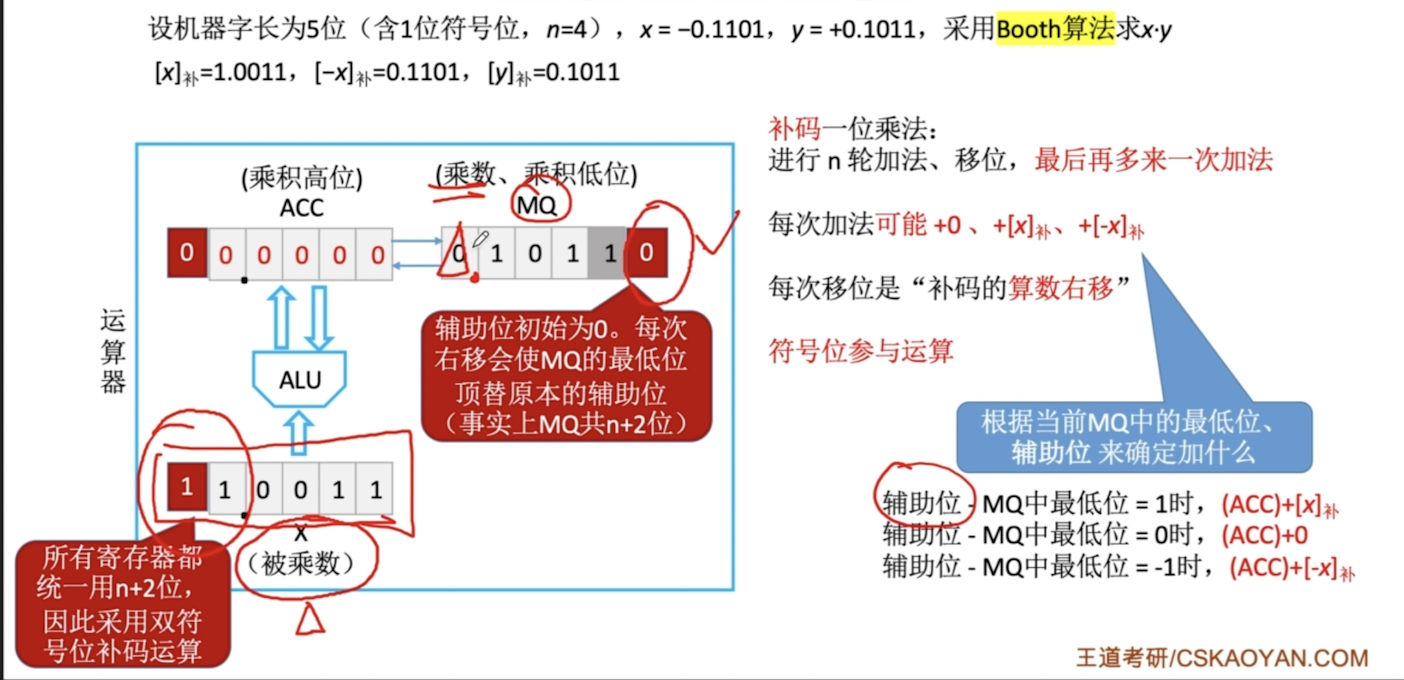
正数的补码：和原码相同

负数的补码：反码末位+1 考虑进位

注意：补码的真值0只有一种表示形式

[x]补 = 1,0000000 表示 x = -2^7

[x]补 = 1.0000000 表示 x = -1

小技巧：已知[x]补，求[-x]补：符号和数值位都取反，末位+1

移码

在补码的基础上将符号位取反

注意：移码只能用于表示整数

移码可以方便地比较大小

2.2.3 移位运算

算数移位

可以用于替代乘法和除法

原码的算数移位

符号位不变，仅对数值位进行移位

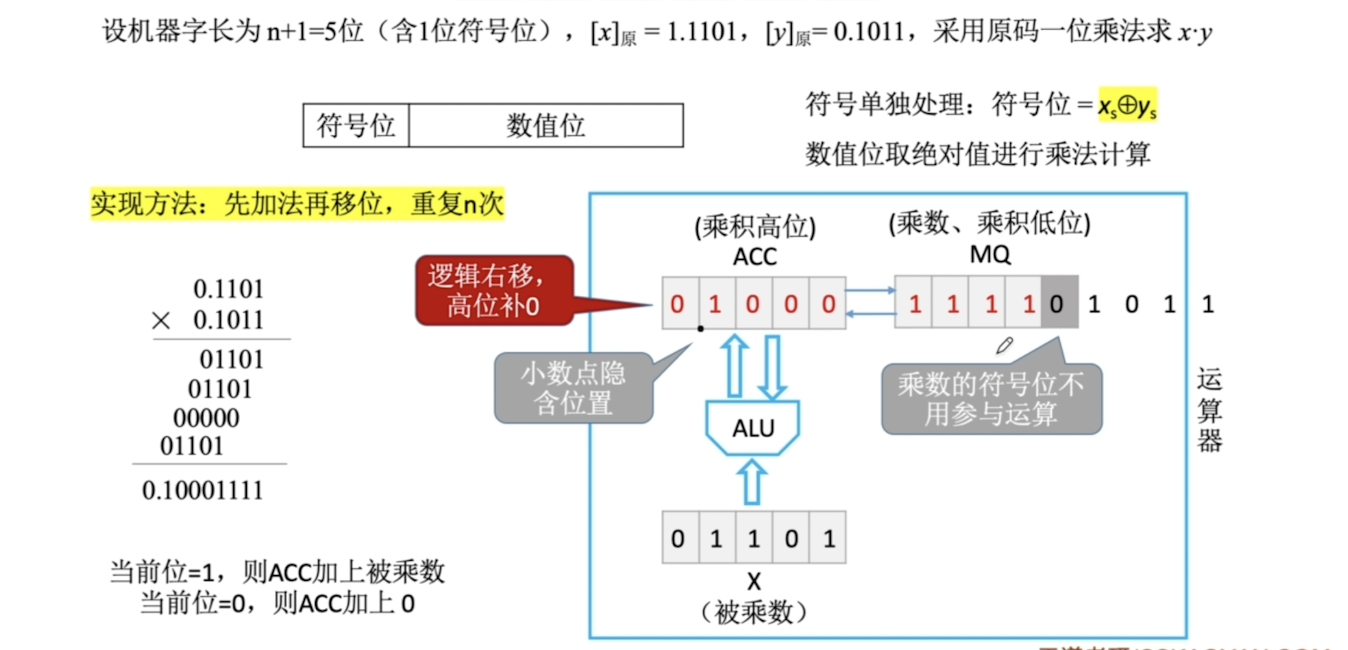
算数右移：高位补0，低位舍弃。如果舍弃位为0，则相当于除以2，否则会丢失精度

算数左移：低位补0，高位舍弃。舍弃0相当于乘以2，否则会丢失

反码的算数移位

正数的反码：右移补0，左移补0

负数的反码：右移补1，左移补1

补码的算数移位

正数的补码：右移补0，左移补0

负数的补码：右移，高位补1；左移低位补0、

逻辑移位

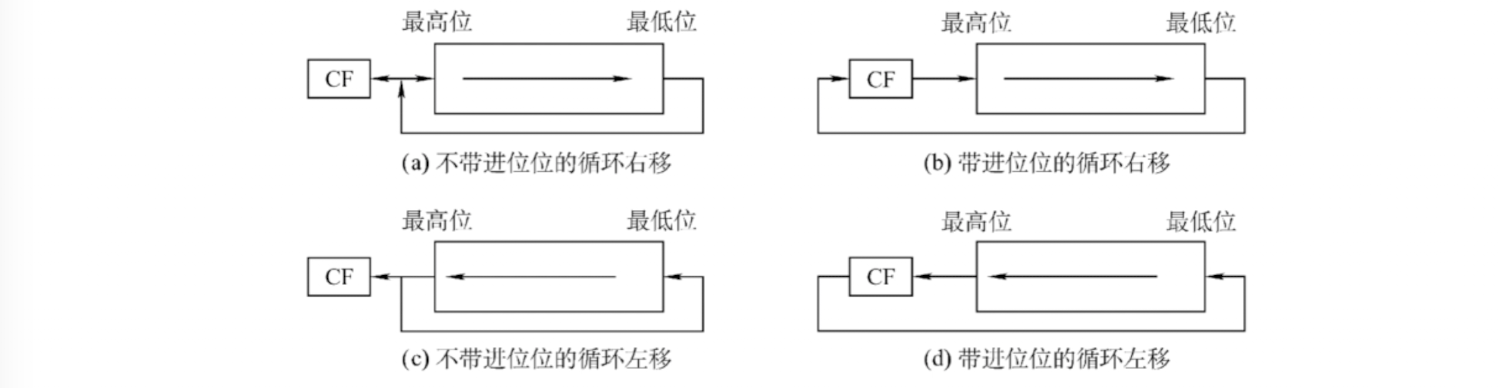
逻辑右移：高位补0，低位舍弃

逻辑左移：低位补0，高位舍弃

循环移位

循环左移：最高位移动到最低位

带进位位的循环左移：数值位最高位进入CF，CF进入最低位

2.2.4 加减运算和溢出判断

补码加减运算

符号位参与运算

[A+B]补 = [A]补 + [B]补

[A-B]补 = [A]补 + [-B]补

小技巧：已知[x]补，求[-x]补：符号和数值位都取反，末位+1

当位数不够时，可能会发生溢出：上溢 / 下溢

溢出判断

只有正数 + 正数才可能上溢；负数 + 负数才可能下溢

法一：采用一位符号位，通过符号位的情况

S = A + B，符号分别为 Sa, Sb, Ss

溢出的情况只有 (0, 0, 1) 和 (1, 1, 0)两种情况

真值表可以解出（数电知识）

V = SaSb(Ss)’ + (Sa)’(Sb)’Ss

V = 1 时溢出，V = 0 没有溢出

法二：采用一位符号位，通过进位情况判断

Cs表示符号位进位，C1表示最高数值位的进位

上溢：Cs = 0， C1 = 1

下溢：Cs = 1， C1 = 0

V = Cs ^ C1 （异或

V = 1 时溢出，V = 0 没有溢出

法三：双符号位

正数为00，负数为11

上溢：01

下溢：10

记 V = S1 ^ S2

V = 1 时溢出，V = 0 没有溢出

双符号位补码又称模4补码；单符号位补码又称：模2补码

符号扩展

为了避免溢出，可以将短数据扩展为长数据

正整数：补0即可

负整数：原码补0，反码和补码补1

正小数：补0即可

负小数：原码和补码补0，反码补1

2.2.5 乘法运算

原码一位乘法

ACC 结果的高位；MQ 被乘数，结果的低位；X乘数
符号位可以单独处理：S = Sx ^ Sy 数值位进行乘法
MQ的最低位就是当前参与运算的位。1的话，ACC+X；0的话ACC+0
每次处理完一位，ACC和MQ整体逻辑右移（高位补0

补码一位乘法

符号位参与运算
右移是算术右移
最后需要多一次加法
被乘数双符号位，乘数单符号位（+一位辅助），部分积双符号位

小技巧：已知[x]补，求[-x]补：符号和数值位都取反，末位+1

2.2.6 除法运算

原码除法

均为逻辑左移

恢复余数法

ACC 被除数、余数；MQ 商；X 除数
符号位单独处理 S = Sx ^ Sy
默认上商1，如果错了，再上商0，恢复余数
每次处理完一位，逻辑左移

加减交替法

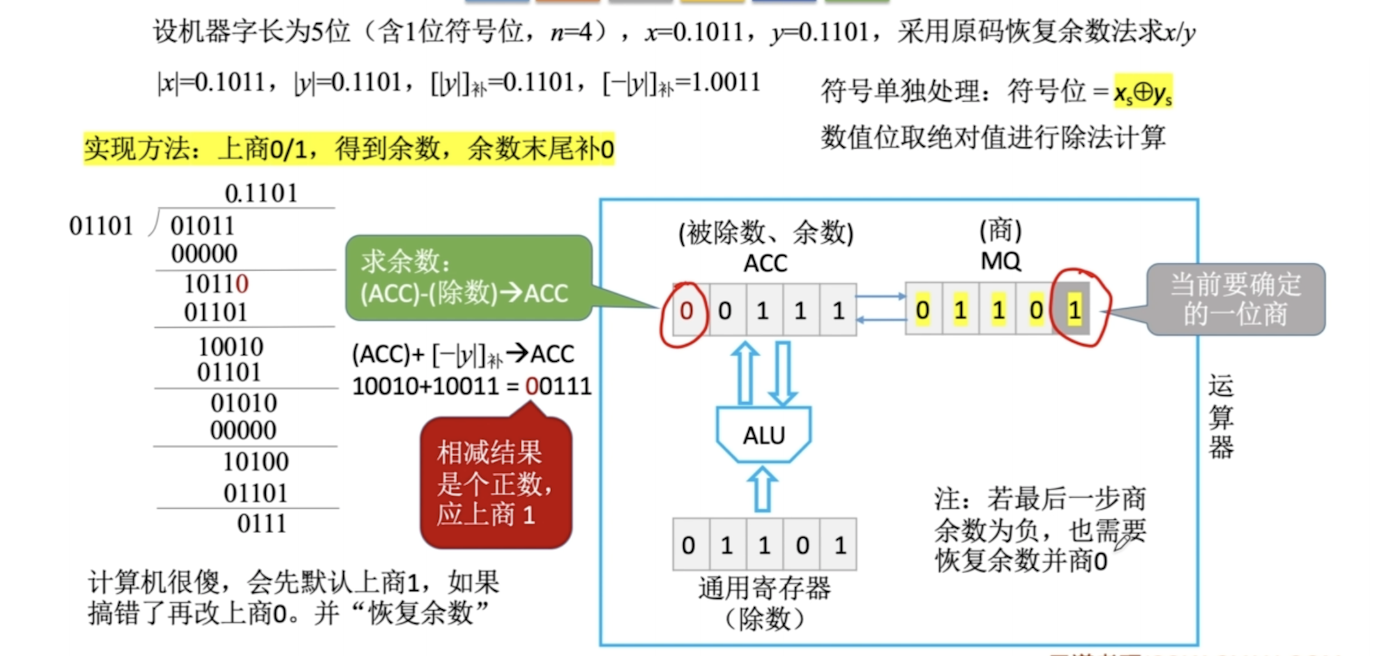
不恢复余数

第一个操作一定是减去除数的绝对值

余数为负，商0并左移，加上除数得到新的余数
余数为正，商1并左移，减去除数得到新的余数

补码除法

加减交替法

符号位参与运算
双符号位

第一步：如果被除数和除数同号，则减掉除数；否则加上除数
余数和除数同号，商1，余数左移一位减掉除数
余数和除数异号，商0，余数左移一位加上除数
重复n次
末尾恒置为1

2.2.7 强制类型转换

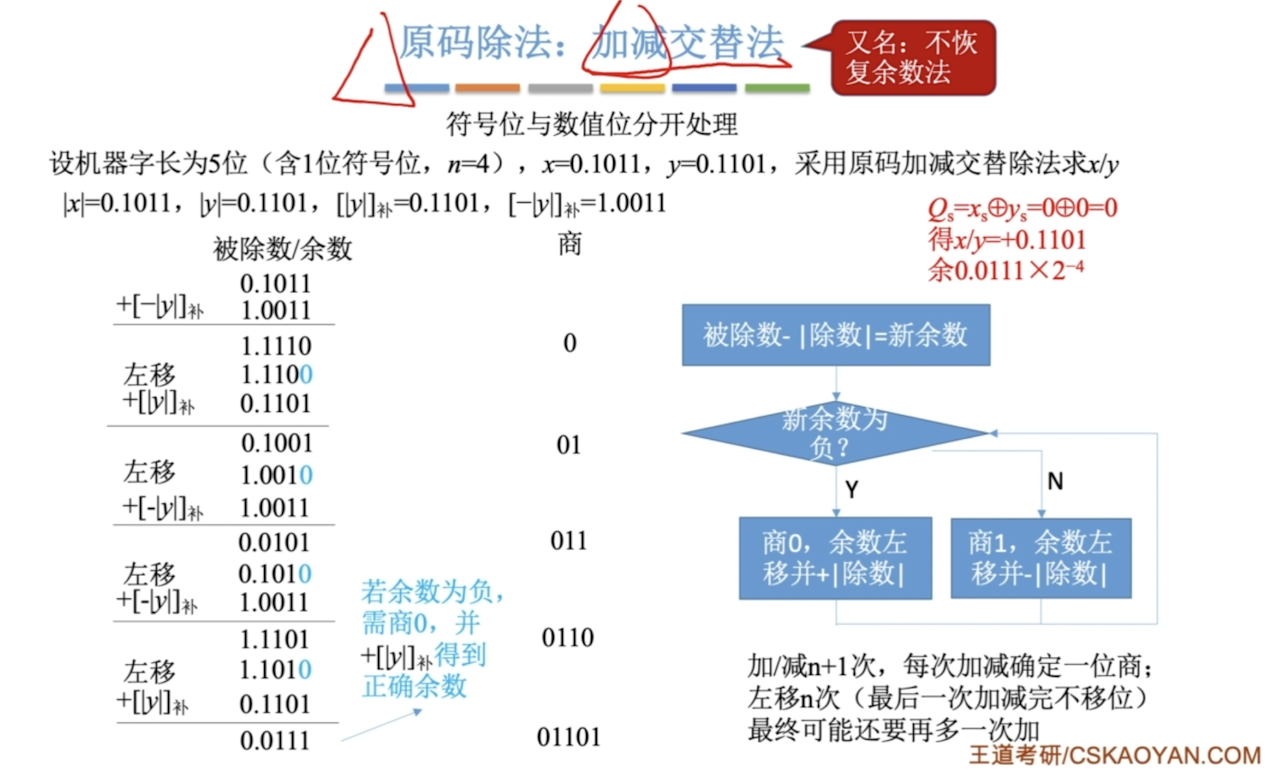
C语言中定点整数用“补码”存储

无符号和有符号整数转换，不改变数据内容，改变解释方式
长整数转短整数，高位截断
短整数变长整数：符号扩展

2.2.8 数据的存储和排列

大小端模式

多字节数据在内存中一定占据连续的几个字节

大端模式：高字节放在低地址

小端模式：低字节放在低地址

边界对齐

2.3.1 浮点数的表示

阶码E表示浮点数的表示范围以及小数点的实际位置

尾数M的数值部分位数反映浮点数的精度

浮点数尾数规格化

最终：让尾数的最高位是有效位

展开全文 >>

leetcode 969. 煎饼排序

2022-02-19

题目

思路

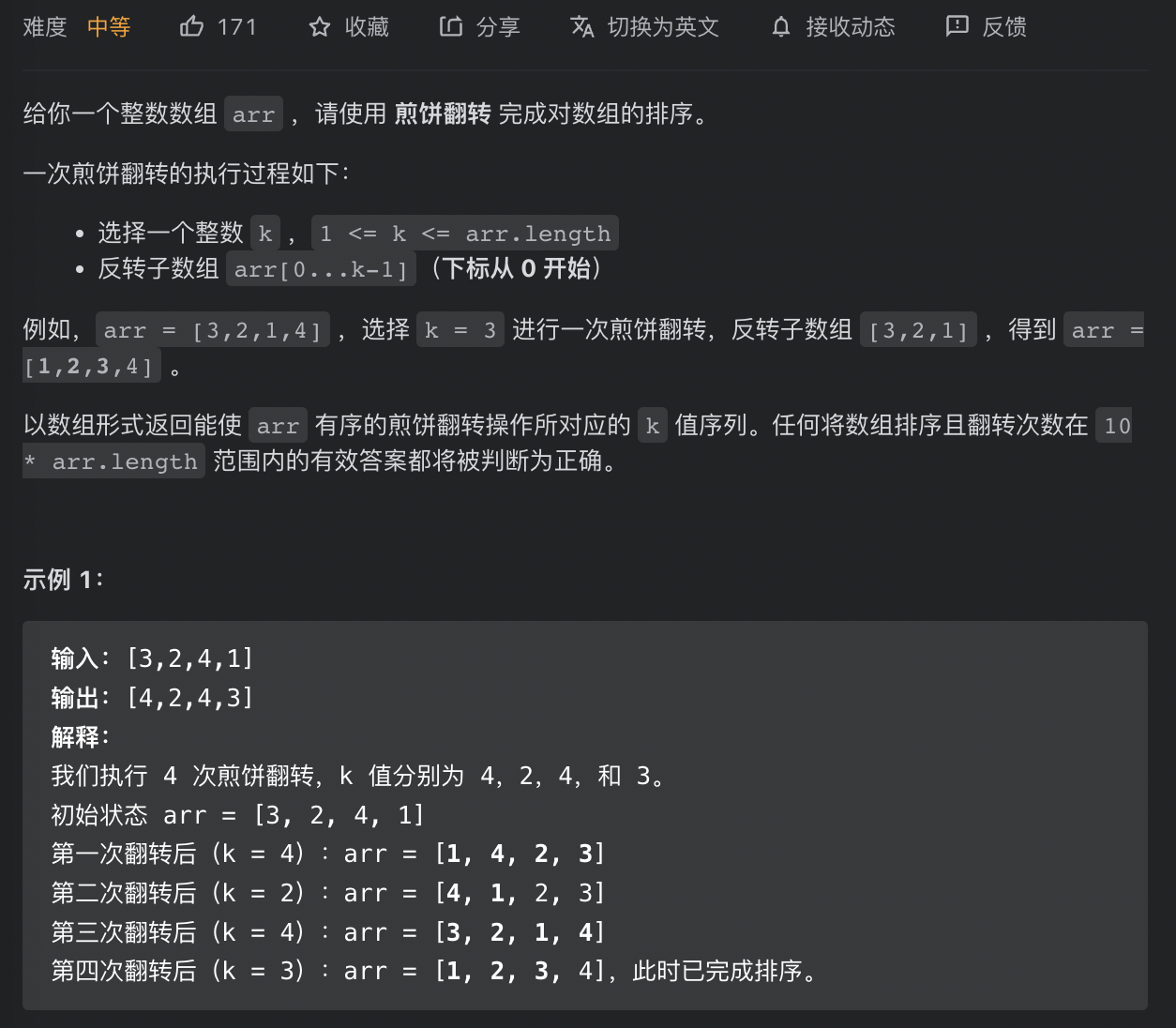
可以借鉴冒泡排序的思想，每次将一个最大值翻转到最后

可以发现，将未排序数组中的最大值index位置翻转到最后的操作是

翻转[0, index]
翻转[0, i] i是未排序数组的末尾

代码

class Solution {
public:
    vector<int> pancakeSort(vector<int>& arr) {
        int len = arr.size();
        vector<int> ans;
        for(int i=len;i>1;--i){
            int index = max_element(arr.begin(), arr.begin()+i)-arr.begin();
            if(index == i-1)  continue;
            reverse(arr.begin(), arr.begin()+index+1);
            ans.push_back(index+1);
            reverse(arr.begin(), arr.begin()+i);
            ans.push_back(i);
        }
        return ans;
    }
};

展开全文 >>

leetcode 1791. 找出星星图的中心节点

2022-02-18

一图流

思路

可以根据题目定义，计算每个节点的度，度为n-1的即为答案
更巧妙的做法是可以发现，中心节点一定在edges的每个元素中都出现，所以随便找两条边，都出现的节点即为答案

展开全文 >>

leetcode 688. 骑士在棋盘上的概率

2022-02-17

题目

来做题

思路

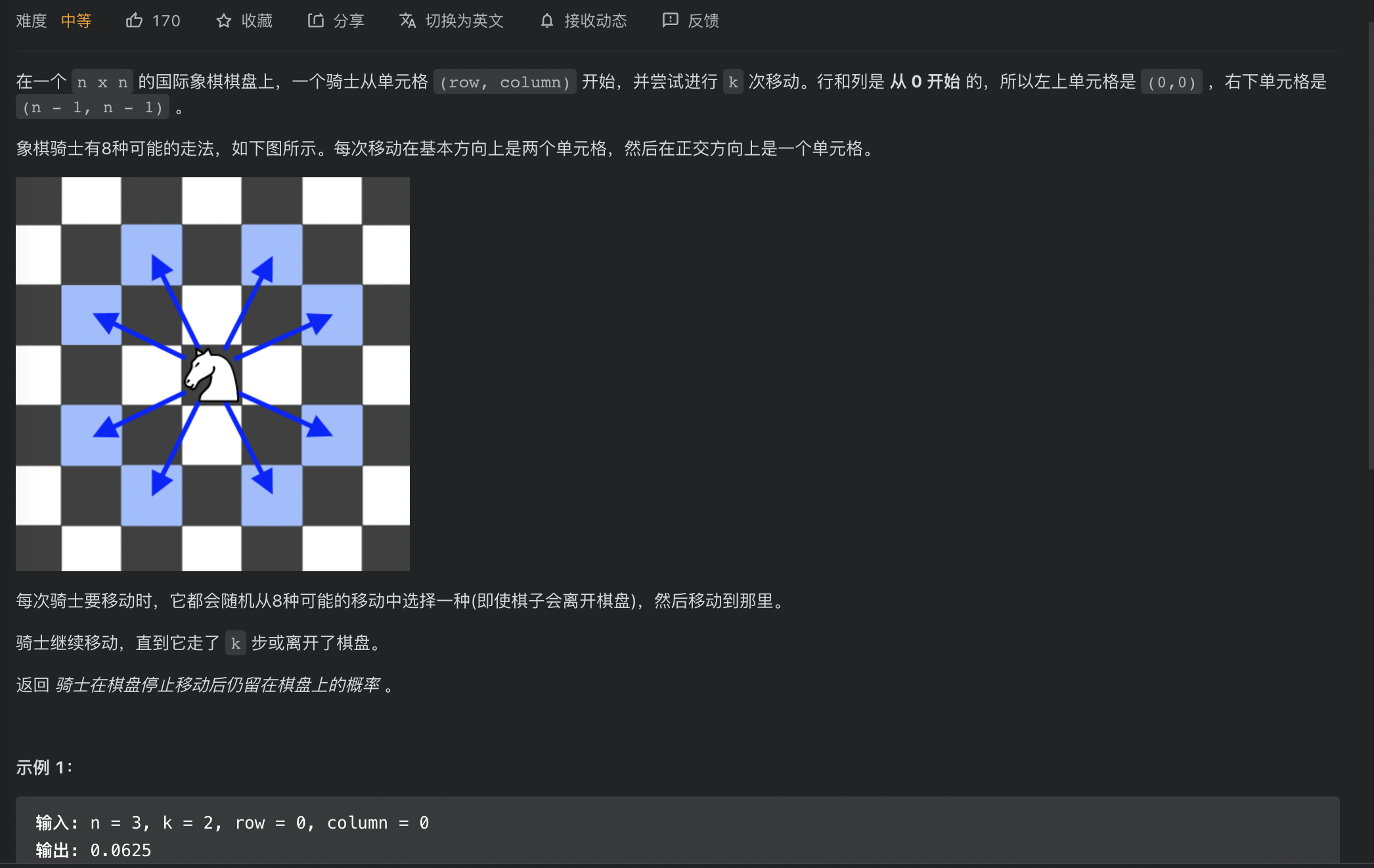
动态规划：考虑到每走一步，结果与上一步的结果有关

定义dp[step][i][j] 表示骑士从i j出发，走了step步后还在棋盘上的概率

那么base case：dp[0][i][j] = 1。走了0步必定停留在棋盘上

状态转移方程呢？由于八个方向都相同概率会走，因此

dp[step][i][j] = 1/8 * SIGMA(dp[step-1][newi][newj])

SIGMA表示求和。转移方程指出：走step步后还在棋盘的概率等于走出一步后，在新位置走step-1步后仍在棋盘的概率

那么代码就简单明了了

技能点：动态规划

代码

class Solution {
    int dx[8] = {-2,-2,-1,1,2,2,1,-1};
    int dy[8] = {-1,1,2,2,1,-1,-2,-2};
public:
    double knightProbability(int n, int k, int row, int column) {
        // dp[step][i][j] 表示从ij出发，走了step步后仍在棋盘上的概率
        vector<vector<vector<double>>> dp(k+1, vector<vector<double>>(n, vector<double>(n)));
        // 规划！
        for(int step=0;step<=k;++step){
            for(int i=0;i<n;++i){
                for(int j=0;j<n;++j){
                    if(step == 0)   dp[step][i][j] = 1; // 走了0步，停留在棋盘上概率为1
                    else
                        for(int k=0;k<8;++k){           // 尝试八个方向
                            int nx = i+dx[k], ny = j+dy[k];
                            if(nx>=0 && nx<n && ny>=0 && ny<n){
                                dp[step][i][j] += dp[step-1][nx][ny]/8; // 状态转移
                            }
                        }
                }
            }
        }
        return dp[k][row][column];
    }
};

展开全文 >>

leetcode 1380. 矩阵中的幸运数

2022-02-15

题目

给你一个 m * n 的矩阵，矩阵中的数字各不相同。请你按任意顺序返回矩阵中的所有幸运数。

幸运数是指矩阵中满足同时下列两个条件的元素：

在同一行的所有元素中最小
在同一列的所有元素中最大

这里做题呢

示例1:
输入：matrix = [[3,7,8],[9,11,13],[15,16,17]]
输出：[15]
解释：15 是唯一的幸运数，因为它是其所在行中的最小值，也是所在列中的最大值。

难度：Easy

思路

简单模拟即可。可以预处理一下矩阵，记录每一行的最小值和每一列的最大值。再逐个元素检查

技能点：模拟

代码

class Solution {
public:
    vector<int> luckyNumbers (vector<vector<int>>& matrix) {
        vector<int> ans;
        int n = matrix.size(), m = matrix[0].size();
        vector<int> row(n, INT_MAX), col(m, 0);
        for(int i=0;i<n;++i){
            for(int j=0;j<m;++j){
                row[i] = min(row[i], matrix[i][j]);
                col[j] = max(col[j], matrix[i][j]);
            }
        }
        for(int i=0;i<n;++i){
            for(int j=0;j<m;++j){
                if(matrix[i][j] == row[i] && matrix[i][j] == col[j]){
                    ans.emplace_back(matrix[i][j]);
                }
            }
        }
        return ans;
    }
};

展开全文 >>

leetcode 204. 计数质数

2022-02-14

题目

给定整数 n ，返回所有小于非负整数 n 的质数的数量。

示例1:
n = 10
输出：4
解释：小于10的质数一共有4个。分别为2 3 5 7

数据量：0 <= n <= 5*10^6

难度：Medium

点这里做题

思路

暴力肯定超时，这里学习一下埃氏筛的做法

用一个isPrime数组标记i是否为质数，如果它是的话，就把2i 3i 4i .. 都标记为非质数

这里可以优化：对于一个质数x，应该从x*x开始标记它的倍数。2x 3x等这些数一定在x之前就被其他数的倍数标记

知识点：埃氏筛

代码

class Solution {
public:
    int countPrimes(int n) {
        vector<int> isPrime(n, 1);
        int ans = 0;
        for(int i=2;i<n;++i){
            if(isPrime[i]){
                ++ans;
                if((long long) i*i < n)
                    for(int j=i*i;j<n;j+=i){
                        isPrime[j] = 0;
                    }
            }
        }
        return ans;
    }
};

展开全文 >>

题目

思路

代码

常用基础知识

数列

三角函数

指数运算

对数运算法则

一元二次方程基础

因式分解

阶乘与双阶乘

常用不等式

#

1.1 函数

一些定义

概念

特殊的函数

反函数

复合函数

基本初等函数

初等函数

参数方程

初等函数的性质

奇偶性

单调性

有界性

周期性

重要结论

1.2 数列极限

定义

性质

1.3 函数极限

定义

性质

1.4 无穷小和无穷大

无穷小

无穷大

无穷小和无穷大的关系

1.5 极限的运算法则

四则运算法则

复合运算极限法则

1.6 极限存在准则 包括两个重要极限

I.夹逼定理

数列的情形

函数的情形

II.单调有界数列必定有极限

两个重要极限

1.7 无穷小的比较

等价无穷小的性质

常见等价无穷小

1.8 函数的连续性和间断点

f(x)在某一点连续连续

f(x)在闭区间连续

间断点及分类

1.9 连续函数的运算和初等函数连续性

连续函数的运算

四则运算

复合运算

初等函数连续性

1.10 闭区间上连续函数的性质

补充

海涅定理

七种未定式极限

2.1.1 进位计数制

进制转换

2.1.2 BCD码

8421码

余3码

2421码

字符和字符串

ASCII码

汉字的表示和编码

大小端

2.1.4 奇偶校验码

校验原理

奇偶校验码

偶校验的硬件实现

2.1.5 海明校验码

海明码求解步骤

海明码纠错

1.6 极限存在准则包括两个重要极限